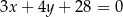Zadanie nr 6339644
Wyznacz równania prostych stycznych do okręgu o równaniu 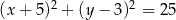 równoległych do prostej o równaniu
równoległych do prostej o równaniu 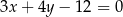 .
.
Rozwiązanie
Dany okrąg to okrąg o środku 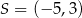 i promieniu
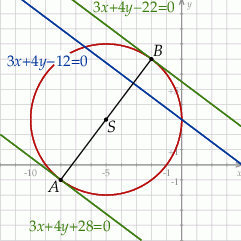
i promieniu 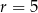 .
.
Sposób I
Wszystkie proste równoległe do danej prostej są postaci 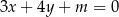 . Jeżeli taka prosta ma być styczna do okręgu, to odległość środka okręgu od tej prostej musi być równa promieniowi okręgu. Korzystając ze wzoru na odległość punktu
. Jeżeli taka prosta ma być styczna do okręgu, to odległość środka okręgu od tej prostej musi być równa promieniowi okręgu. Korzystając ze wzoru na odległość punktu 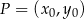 od prostej
od prostej 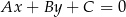 :
:
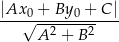
otrzymujemy więc równanie.
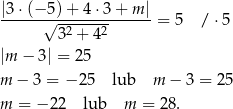
Szukane styczne mają więc równania 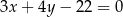 i
i 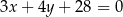 .
.
Sposób II
Dana prosta ma współczynnik kierunkowy 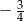 , więc proste równoległe do niej mają równanie postaci
, więc proste równoległe do niej mają równanie postaci 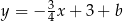 (dodajemy 3-kę, żeby nam się skróciła w równaniu okręgu). Sprawdzamy teraz, kiedy taka prosta ma dokładnie jeden punkt wspólny z danym okręgiem – podstawiamy
(dodajemy 3-kę, żeby nam się skróciła w równaniu okręgu). Sprawdzamy teraz, kiedy taka prosta ma dokładnie jeden punkt wspólny z danym okręgiem – podstawiamy 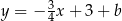 do równania okręgu.
do równania okręgu.
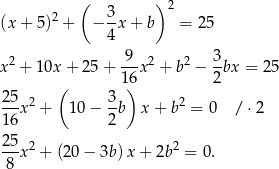
Jeżeli powyższe równanie ma mieć jedno rozwiązanie, to musi być 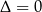 . Sprawdzamy, kiedy tak jest.
. Sprawdzamy, kiedy tak jest.
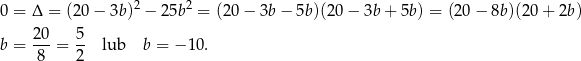
Szukane styczne mają więc równania
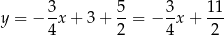
i
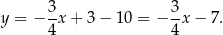
Sposób III
Tym razem najpierw wyznaczymy punkty styczności 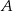 i
i 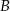 szukanych stycznych z okręgiem. Dana prosta ma współczynnik kierunkowy
szukanych stycznych z okręgiem. Dana prosta ma współczynnik kierunkowy 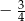 , więc proste prostopadłe do danej prostej mają równanie postaci
, więc proste prostopadłe do danej prostej mają równanie postaci 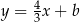 . Podstawiamy teraz w tym równaniu współrzędne punktu
. Podstawiamy teraz w tym równaniu współrzędne punktu 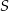 .
.
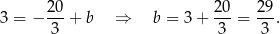
Szukamy teraz punktów wspólnych prostej 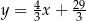 z okręgiem.
z okręgiem.
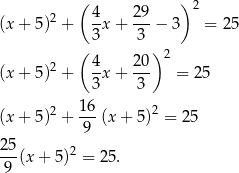
Mamy stąd
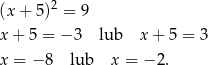
Stąd odpowiednio 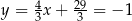 i
i 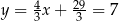 . Zatem interesujące nas punkty styczności to
. Zatem interesujące nas punkty styczności to 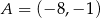 i
i 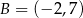 .
.
Teraz korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/6339644/HzadR31x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 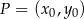
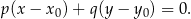
W naszej sytuacji ![→v = [3 ,4]](https://img.zadania.info/zad/6339644/HzadR34x.gif) (wektor prostopadły do danej prostej) i
(wektor prostopadły do danej prostej) i 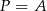 lub
lub 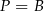 . Równania stycznych mają więc postać
. Równania stycznych mają więc postać
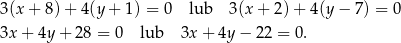
Odpowiedź: 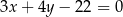 i
i