Zadanie nr 9525142
Z punktu 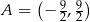 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 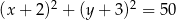 . Oblicz pole trójkąta
. Oblicz pole trójkąta 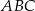 , gdzie
, gdzie 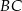 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku – dany okrąg to okrąg o środku 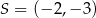 i promieniu
i promieniu 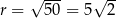 .
.
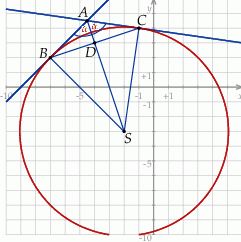
Sposób I
Jeżeli oznaczymy przez 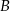 i
i 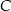 punkty styczności stycznych poprowadzonych z punktu
punkty styczności stycznych poprowadzonych z punktu 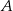 do okręgu, to
do okręgu, to
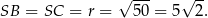
Ponadto
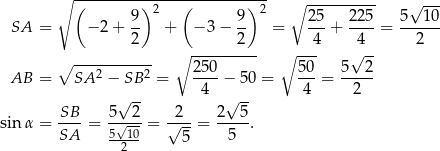
Teraz patrzymy na trójkąt prostokątny 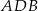 i obliczamy długości odcinków
i obliczamy długości odcinków 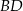 i
i 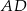 .
.
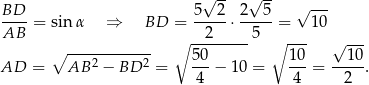
Pozostało obliczyć pole trójkąta 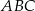 .
.
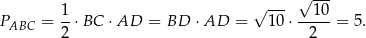
Sposób II
Tak jak poprzednio zauważamy, że
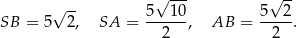
To pozwala obliczyć pole trójkąta prostokątnego 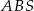 .
.
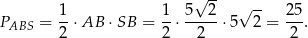
Trójkąty prostokątne 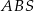 i
i 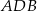 mają wspólny kąt przy wierzchołku
mają wspólny kąt przy wierzchołku 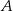 , więc są podobne. Skala tego podobieństwa jest równa
, więc są podobne. Skala tego podobieństwa jest równa
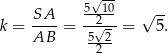
Pole zmienia się jak kwadrat skali podobieństwa, więc
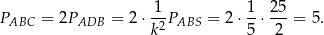
Sposób III
Tak jak poprzednio zauważamy, że
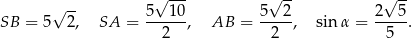
Mamy ponadto
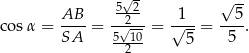
To pozwala obliczyć 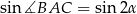 .
.
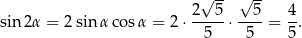
Liczymy teraz pole trójkąta 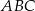 (korzystamy ze wzoru z sinusem).
(korzystamy ze wzoru z sinusem).
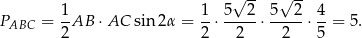
Sposób IV
Tym razem użyjemy odrobinę więcej geometrii analitycznej i wyznaczymy równania stycznych.
Proste przechodzące przez punkt 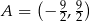 mają postać
mają postać 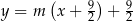 (tak naprawdę brakuje w tym pęku pionowej prostej
(tak naprawdę brakuje w tym pęku pionowej prostej 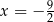 , ale łatwo sprawdzić, że nie jest ona szukaną styczną). Sprawdźmy, kiedy prosta tej postaci
, ale łatwo sprawdzić, że nie jest ona szukaną styczną). Sprawdźmy, kiedy prosta tej postaci
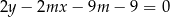
jest styczna do okręgu: sprawdzamy kiedy jej odległość od punktu 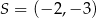 jest równa
jest równa 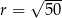 .
.
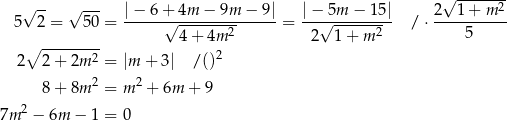
Rozwiązujemy otrzymane równanie kwadratowe
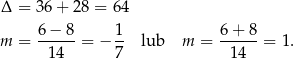
Zatem styczne do okręgu przechodzące przez punkt 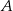 mają postać
mają postać
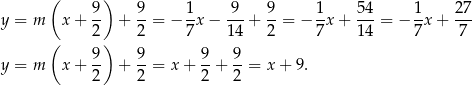
Znajdźmy punkty wspólne tych stycznych z okręgiem. Najpierw pierwsza styczna
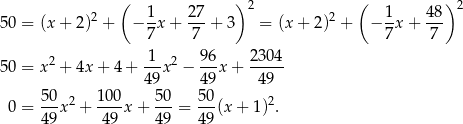
Zatem 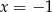 ,
, 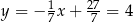 i
i 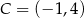 . Szukamy teraz punktu wspólnego drugiej stycznej z okręgiem
. Szukamy teraz punktu wspólnego drugiej stycznej z okręgiem
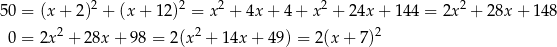
Stąd 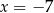 ,
, 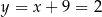 i
i 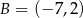 . Teraz obliczamy pole trójkąta
. Teraz obliczamy pole trójkąta 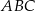 korzystając ze wzoru
korzystając ze wzoru
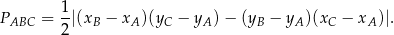
Liczymy
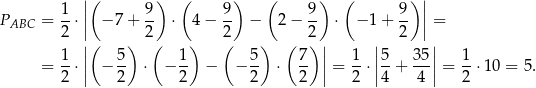
Odpowiedź: 5

