/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Udowodnij...

Zadanie nr 7956124

Dodaj do ulubionych
Dodaj do rozwiązanych

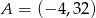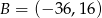Dane są punkty A = (− 4,32) i B = (−3 6,16) . Wykaż, że koło o średnicy 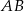AB jest zawarte w II ćwiartce prostokątnego układu współrzędnych.

Rozwiązanie

Środek odcinka 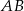AB (a więc również środek koła) ma współrzędne

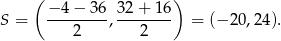
( − 4 − 36 32+ 16) S = ---------,-------- = (− 20,2 4). 2 2

Zatem promień koła to

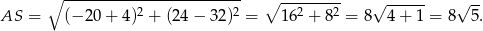
∘ ------------------------- ∘ --------- √ ------ √ -- AS = (− 20+ 4)2 + (2 4− 32)2 = 16 2 + 82 = 8 4+ 1 = 8 5.

W tym miejscu warto sobie naszkicować o co chodzi w zadaniu (liczby są duże, ale tu naprawdę wystarczy szkic, żeby zobaczyć co mamy zrobić).

PIC

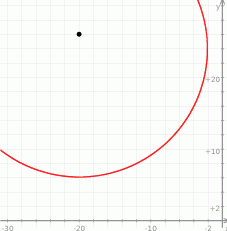
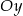Jak się przyjrzymy, to widać, że wystarczy wykazać, że środek okręgu jest oddalony od osi Ox i Oy o więcej niż 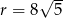√ -- r = 8 5 . To zaś sprowadza się do nierówności

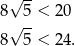
√ -- 8 5 < 20 √ -- 8 5 < 24 .

Ponieważ 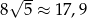√ -- 8 5 ≈ 17,9 obie nierówności są spełnione.

Wersja PDF