/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Udowodnij...

Zadanie nr 9292717

Dodaj do ulubionych
Dodaj do rozwiązanych

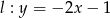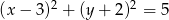Wykaż, że prosta l : y = − 2x − 1 jest styczna do okręgu 2 2 (x − 3) + (y + 2) = 5 .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

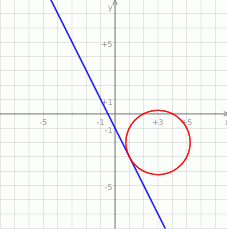
Sposób I

Przypomnijmy, że prosta może mieć z okręgiem jeden lub dwa lub zero punktów wspólnych. Ponadto prosta jest styczna do okręgu jeżeli ma z nim dokładnie jeden punkt wspólny. Wyznaczamy punkty wspólne okręgu i prostej

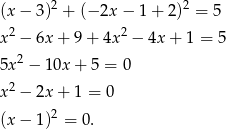
(x − 3)2 + (− 2x − 1 + 2 )2 = 5 x 2 − 6x + 9+ 4x2 − 4x + 1 = 5 2 5x − 10x + 5 = 0 x 2 − 2x + 1 = 0 2 (x − 1) = 0.

Zatem prosta z okręgiem ma dokładnie punkt wspólny 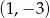(1,− 3) , czyli jest styczna.

Sposób II

Wyznaczamy środek i promień okręgu

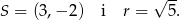
√ -- S = (3,− 2) i r = 5.

Jeżeli prosta l jest styczna do okręgu to jej odległość od środka tego okręgu będzie równa promieniowi okręgu. Liczymy (korzystamy ze wzoru na odległość punktu od prostej)

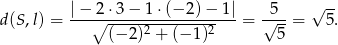
√ -- d(S,l) = |-−∘2-⋅3−--1⋅(−-2)-−-1| = √5--= 5 . (−2 )2 + (− 1)2 5

Zatem prosta i okrąg są styczne

Wersja PDF