Zadanie nr 1093339

Uzasadnij, że jeżeli 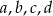a,b,c,d są liczbami dodatnimi to

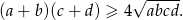
√ ----- (a + b)(c + d) ≥ 4 abcd.

Rozwiązanie

Sposób I

Na mocy nierówności

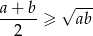
a+ b √ --- ------≥ ab 2

między średnią arytmetyczną i geometryczną mamy

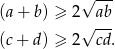
(a+ b) ≥ 2√ab-- √ --- (c+ d) ≥ 2 cd.

Mnożąc te nierówności stronami mamy

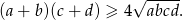
----- (a + b)(c + d) ≥ 4 √ abcd.

Sposób II

Podnieśmy daną nierówność stronami do kwadratu

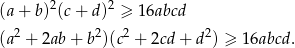
(a+ b)2(c+ d )2 ≥ 16abcd 2 2 2 2 (a + 2ab+ b )(c + 2cd+ d ) ≥ 16abcd .

Teraz wystarczy zauważyć, że

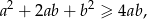
2 2 a + 2ab + b ≥ 4ab,

bo nierówność ta jest równoważna nierówności

2 (a− b ) ≥ 0.

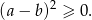
Podobnie

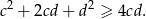
c2 + 2cd+ d2 ≥ 4cd.

Mnożąc te dwie nierówności stronami otrzymamy żądaną nierówność.

Sposób III

Jak poprzednio, podnosimy nierówność stronami do kwadratu i mamy

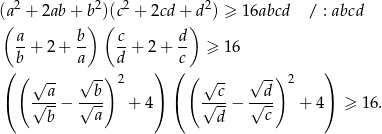
2 2 2 2 ((a + 2ab+ b) )((c + 2cd+ )d ) ≥ 16abcd / : abcd a- b- c- d- b + 2 + a d + 2 + c ≥ 16 ( ( √ -) ) ( ( √ -) ) √a-- b 2 √c- d 2 ( √---− √--- + 4) ( √---− √--- + 4) ≥ 16 . b a d c

A ostatnia nierówność jest oczywiście spełniona, bo wyrażenie w każdym z nawiasów jest nie mniejsze niż 4.

Sposób IV

Wymnażając nawiasy z lewej strony nierówności mamy

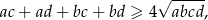
√ ----- ac+ ad+ bc+ bd ≥ 4 abcd ,

a tę nierówność łatwo uzasadnić korzystając z nierówności między średnimi: arytmetyczną i geometryczną dla 4 liczb.

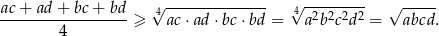
ac + ad + bc + bd 4√ -------------- 4√ --------- √ ----- ------------------≥ ac⋅ad ⋅bc ⋅bd = a2b2c2d2 = abcd. 4

Sposób V

Wymnażając nawiasy z lewej strony nierówności mamy

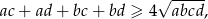
√ ----- ac+ ad+ bc+ bd ≥ 4 abcd ,

Wystarczy teraz zauważyć, że

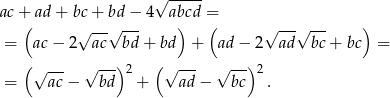
----- ac + ad + bc + bd − 4√ abcd = ( √ --√ --- ) ( √ ---√ --- ) = ac− 2 ac bd + bd + ad − 2 ad bc+ bc = ( √ --- √ --) 2 ( √ --- √ --)2 = ac− bd + ad− bc .

Sposób VI

Wymnażając nawiasy z lewej strony nierówności mamy

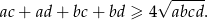
√ ----- ac+ ad+ bc+ bd ≥ 4 abcd .

Podnosimy teraz nierówność stronami do kwadratu.

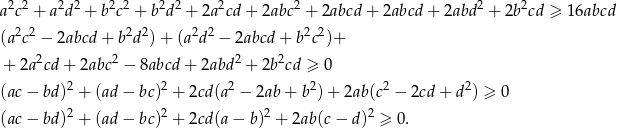
2 2 2 2 2 2 2 2 2 2 2 2 a c + a d + b c + b d + 2a cd+ 2abc + 2abcd + 2abcd + 2abd + 2b cd ≥ 16abcd (a2c2 − 2abcd + b2d2) + (a2d2 − 2abcd + b2c2)+ 2 2 2 2 + 2a cd+ 2abc − 8abcd + 2abd + 2b cd ≥ 0 (ac− bd)2 + (ad− bc)2 + 2cd(a2 − 2ab + b2)+ 2ab(c2 − 2cd + d2) ≥ 0 (ac− bd)2 + (ad− bc)2 + 2cd(a − b)2 + 2ab(c− d)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musi być prawdziwa.