/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 1283311

Dodaj do ulubionych
Dodaj do rozwiązanych

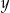Wykaż, że dla dowolnych liczb rzeczywistych x i y takich, że 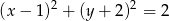(x − 1)2 + (y + 2)2 = 2 , prawdziwa jest nierówność y + 1 ≤ x .

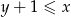Rozwiązanie

Sposób I

Zauważmy, że równanie 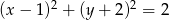(x − 1)2 + (y + 2)2 = 2 opisuje na płaszczyźnie okrąg o środku 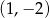(1,− 2) i promieniu 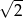√ -- 2 . Nierówność 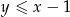y ≤ x − 1 opisuje natomiast półpłaszczyznę znajdującą się poniżej prostej 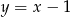y = x− 1 . Sprawdźmy, ile punktów wspólnych ma ta prosta z danym okręgiem.

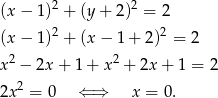
2 2 (x − 1) + (y + 2) = 2 (x − 1)2 + (x − 1 + 2)2 = 2 2 2 x − 2x + 1 + x + 2x + 1 = 2 2x2 = 0 ⇐ ⇒ x = 0 .

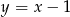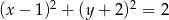To oznacza, że prosta y = x − 1 jest styczna do okręgu 2 2 (x − 1) + (y+ 2) = 2 .

PIC

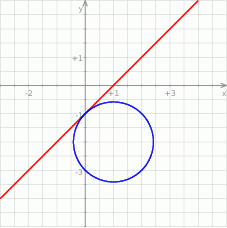
Gdy naszkicujemy tę sytuację, to widać, że wszystkie punkty tego okręgu rzeczywiście znajdują się poniżej prostej 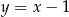y = x − 1 .

Sposób II

Tym razem skorzystamy z prostej do uzasadnienia nierówności między średnią arytmetyczną i kwadratową.

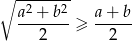
∘ -2----2- a--+-b- ≥ a+--b- 2 2

Równość daną w treści zadania możemy zapisać w postaci

∘ -------2----------2- 1 = (x-−-1)--+-(y-+-2)- = 2 ∘ -------2----------2- = (1-−-x)--+-(y-+-2)- ≥ 1−--x+--y+--2- / ⋅ 2 2 2 2 ≥ 3− x+ y x ≥ y+ 1.
Wersja PDF