/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 2683674

Dodaj do ulubionych
Dodaj do rozwiązanych

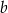Wykaż, że dla każdej liczby rzeczywistej a różnej od 0 i każdej liczby rzeczywistej b różnej od 0 spełniona jest nierówność

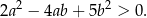
2a2 − 4ab + 5b2 > 0 .

Rozwiązanie

Sposób I

Przekształcamy daną nierówność w sposób równoważny

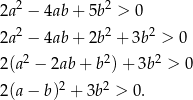
2 2 2a − 4ab + 5b > 0 2a2 − 4ab + 2b2 + 3b2 > 0 2 2 2 2(a − 2ab+ b )+ 3b > 0 2(a− b)2 + 3b2 > 0.

Teraz jest jasne, że nierówność ta jest zawsze spełniona.

Sposób II

Przekształcamy daną nierówność w sposób równoważny

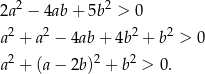
2a2 − 4ab + 5b2 > 0 2 2 2 2 a + a − 4ab+ 4b + b > 0 a2 + (a− 2b)2 + b2 > 0.

Teraz jest jasne, że nierówność ta jest zawsze spełniona.

Wersja PDF