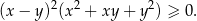/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 2847863

Dodaj do ulubionych
Dodaj do rozwiązanych

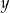Uzasadnij, że dla dowolnych liczb dodatnich x i y prawdziwa jest nierówność

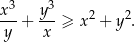
3 3 x--+ y--≥ x2 + y2. y x

Rozwiązanie

Przekształcamy nierówność w sposób równoważny.

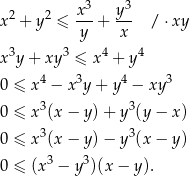
3 3 x2 + y2 ≤ x--+ y-- /⋅ xy y x x3y + xy 3 ≤ x4 + y4 0 ≤ x4 − x3y + y 4 − xy 3 3 3 0 ≤ x (x − y )+ y (y− x) 0 ≤ x3(x − y )− y 3(x− y) 3 3 0 ≤ (x − y )(x − y ).

Sposób I

Nierówność jest oczywiście spełniona, gdy 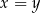x = y . Jeżeli 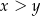x > y , to oba wyrażenia po prawej stronie są dodatnie, więc ich iloczyn jest dodatni. Jeżeli w końcu 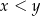x < y , to oba wyrażenia po prawej stronie nierówności są ujemne i ich iloczyn też jest dodatni.

Sposób II

Zauważmy, że

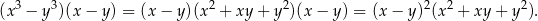
3 3 2 2 2 2 2 (x − y )(x − y) = (x − y)(x + xy + y )(x− y) = (x − y) (x + xy + y ).

Oczywiście oba otrzymane wyżej wyrażenia są nieujemne, więc

2 2 2 (x − y )(x + xy + y ) ≥ 0.
Wersja PDF