Zadanie nr 3439933
Uzasadnij, że jeśli liczby rzeczywiste 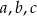 spełniają nierówności:
spełniają nierówności: 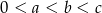 , to
, to
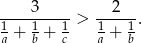
Rozwiązanie
Sposób I
Przekształcamy daną nierówność
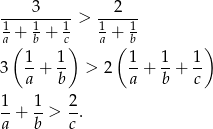
Zauważmy teraz, że z założenia 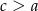 i
i 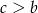 , więc rzeczywiście
, więc rzeczywiście
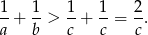
Sposób II
Przekształcamy daną nierówność
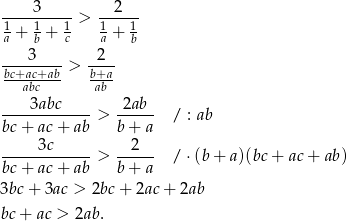
Zauważmy teraz, że z założenia 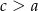 i
i 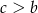 , więc
, więc
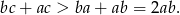
To oznacza, że wyjściowa nierówność też jest spełniona (bo przekształcaliśmy ją w sposób równoważny).

