Zadanie nr 4051962
Funkcja 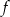 określona jest wzorem
określona jest wzorem 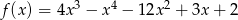 dla
dla 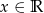 . Wykaż, że
. Wykaż, że
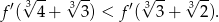
Rozwiązanie
Liczymy pochodną danej funkcji
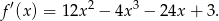
Zauważmy teraz, że
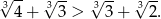
Wystarczy zatem udowodnić, że funkcja 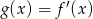 jest funkcją malejącą. W tym celu liczymy pochodną funkcji
jest funkcją malejącą. W tym celu liczymy pochodną funkcji 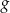 (czyli drugą pochodną funkcji
(czyli drugą pochodną funkcji 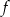 ).
).
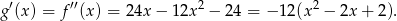
Ponieważ trójmian w nawiasie jest stale dodatni (bo 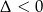 ), to
), to 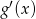 jest stale ujemna. To oznacza, że funkcja
jest stale ujemna. To oznacza, że funkcja 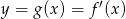 rzeczywiście jest funkcją malejącą. W szczególności
rzeczywiście jest funkcją malejącą. W szczególności