/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 4917280

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest nierówność

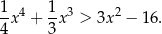
1 1 -x 4 +--x3 > 3x 2 − 1 6. 4 3

Rozwiązanie

Musimy udowodnić, że

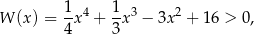
1 1 W (x) = --x4 + -x3 − 3x 2 + 1 6 > 0, 4 3

Aby to zrobić liczymy pochodną lewej strony.

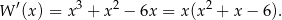
′ 3 2 2 W (x ) = x + x − 6x = x (x + x− 6).

Rozkładamy jeszcze trójmian w nawiasie.

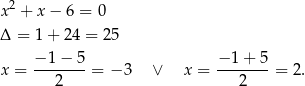
2 x + x − 6 = 0 Δ = 1+ 24 = 25 − 1− 5 − 1+ 5 x = -------= − 3 ∨ x = ------- = 2. 2 2

Mamy zatem

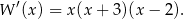
′ W (x) = x(x+ 3)(x − 2).

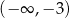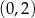Pochodna jest więc ujemna w przedziałach (− ∞ ,− 3) i (0,2) , oraz dodatnia w przedziałach 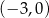(− 3,0 ) i (2 ,+∞ ) .

PIC

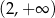To oznacza, że funkcja 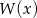W (x) maleje w przedziale 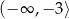(− ∞ ,− 3⟩ do wartości

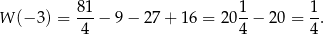
W (− 3) = 81-− 9− 27+ 16 = 20 1− 20 = 1-. 4 4 4

Następnie funkcja rośnie do wartości

W (0) = 16,

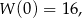
potem znów maleje do wartości

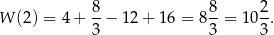
8 8 2 W (2) = 4+ --− 12 + 16 = 8 --= 1 0-. 3 3 3

Następnie funkcja rośnie w przedziale 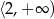⟨2,+ ∞ ) . Przeprowadzona analiza dowodzi, że funkcja 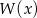W (x) nie przyjmuje wartości ujemnych.

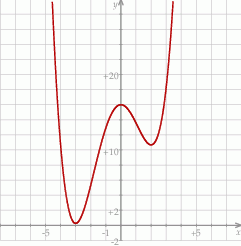
Na koniec wykres funkcji 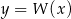y = W (x) dla ciekawskich.

PIC

Wersja PDF