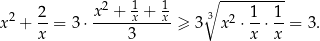/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 5194122

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że funkcja 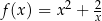2 2 f (x) = x + x przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.

Rozwiązanie

Sposób I

Wystarczy pokazać, zbiór rozwiązań nierówności

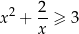
x 2 + 2-≥ 3 x

zawiera wszystkie liczby dodatnie. Liczymy

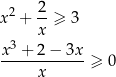
x2 + 2-≥ 3 x x3 + 2 − 3x -----x------≥ 0

Aby rozłożyć licznik szukamy jego miejsc zerowych. Łatwo znaleźć pierwiastek 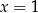x = 1 . Dzielimy licznik przez 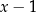x − 1 . My zrobimy to grupując wyrazy

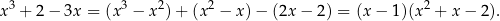
x 3 + 2− 3x = (x3 − x2) + (x2 − x) − (2x − 2) = (x− 1)(x2 + x− 2).

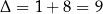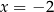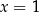Rozkładamy trójmian w nawiasie, Δ = 1 + 8 = 9 , x = −2 lub x = 1 . Możemy więc zapisać naszą nierówność w postaci

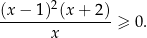
2 (x-−-1)-(x-+-2)-≥ 0. x

Ta nierówność jest oczywiście spełniona przez każdą liczbę dodatnią (bo każdy składnik jest nieujemny).

Na koniec, dla ciekawkich, wykres funkcji 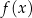f(x)

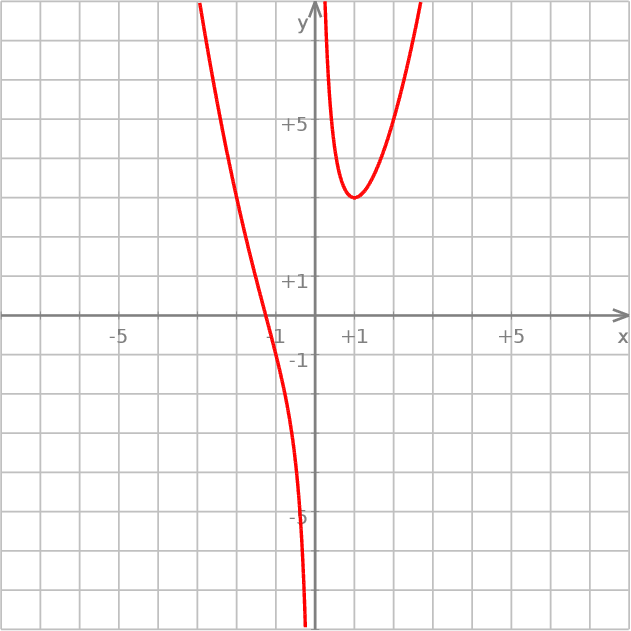
ZINFO-FIGURE

Sposób II

Przy założeniu, że 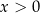x > 0 możemy interesującą nas nierówność przekształcić w następujący sposób:

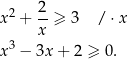
2 x2 + -- ≥ 3 / ⋅x x x3 − 3x + 2 ≥ 0.

Wielomian z lewej strony rozkładamy tak samo jak w poprzednim sposobie i otrzymujemy nierówność

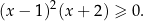
2 (x − 1) (x + 2) ≥ 0.

Otrzymana nierówność jest zawsze spełniona (bo 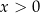x > 0 ), więc wyjściowa nierówność też musiała być spełniona (bo przekształcaliśmy ją w sposób równoważny).

Sposób III

Na mocy nierówności

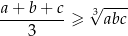
a-+-b-+-c 3√ ---- 3 ≥ abc

między średnimi arytmetyczną i geometryczną liczb dodatnich mamy

x2 + 1 + 1 ∘ --------- x2 + 2-= 3⋅ -----x---x-≥ 3 3x 2 ⋅ 1-⋅ 1-= 3. x 3 x x
Wersja PDF