/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 5730621

Dodaj do ulubionych
Dodaj do rozwiązanych

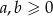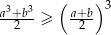Udowodnij, że jeżeli a ,b ≥ 0 , to prawdziwa jest nierówność 3 3 ( )3 a+2b--≥ a+2b- .

Rozwiązanie

Sposób I

Przekształcamy nierówność w sposób równoważny korzystając ze wzoru na sumę sześcianów.

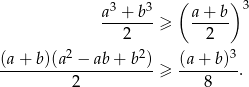
3 3 ( ) 3 a-+--b- a-+-b- 2 ≥ 2 2 2 3 (a-+-b)(a-−--ab+--b-) ≥ (a-+-b)- . 2 8

Jeżeli 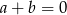a+ b = 0 , to nierówność jest oczywiście spełniona, więc możemy założyć, że 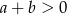a + b > 0 . Przy tym założeniu możemy nierówność podzielić stronami przez (a + b) .

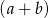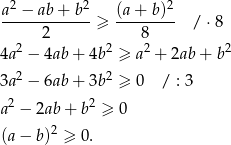
a-2 −-ab-+-b2 (a+--b)2 2 ≥ 8 / ⋅8 2 2 2 2 4a − 4ab + 4b ≥ a + 2ab+ b 3a2 − 6ab + 3b 2 ≥ 0 / : 3 a2 − 2ab + b2 ≥ 0 2 (a − b) ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być prawdziwa.

Sposób II

Przekształcamy nierówność w sposób równoważny korzystając ze wzoru na sześcian sumy.

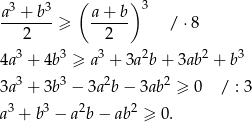
( ) 3 a3 +-b3 a-+-b- 2 ≥ 2 / ⋅8 3 3 3 2 2 3 4a + 4b ≥ a + 3a b + 3ab + b 3a3 + 3b3 − 3a2b− 3ab2 ≥ 0 / : 3 a3 + b3 − a 2b− ab 2 ≥ 0.

Rozkładamy teraz lewą stronę na czynniki – grupujemy wyrazy tak, żeby wyłączyć 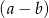(a − b) przed nawias.

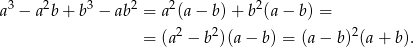
a3 − a2b+ b3 − ab 2 = a2(a− b)+ b2(a− b) = 2 2 2 = (a − b )(a− b ) = (a− b) (a+ b).

Otrzymane wyrażenie jest oczywiście nieujemne.

Sposób III

Tak jak poprzednio przekształcamy nierówność do postaci

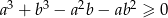
a 3 + b3 − a2b − ab2 ≥ 0

Tym razem rozkładamy lewą stroną korzystając ze wzoru na sumę sześcianów.

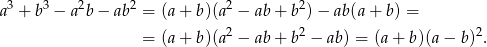
3 3 2 2 2 2 a + b − a b − ab = (a+ b)(a − ab+ b )− ab (a+ b ) = = (a+ b)(a2 − ab+ b2 − ab ) = (a+ b)(a− b)2.

Otrzymane wyrażenie jest oczywiście nieujemne.

Sposób IV

Tak jak poprzednio przekształcamy nierówność do postaci

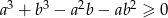
3 3 2 2 a + b − a b − ab ≥ 0

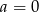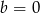Jeżeli a = 0 lub b = 0 to nierówność jest oczywiście spełniona, więc załóżmy, że 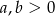a,b > 0 . Przy tym założeniu możemy nierówność podzielić stronami przez 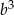b3 i podstawić t = ab .

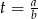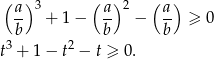
( )3 ( )2 ( ) a- + 1− a- − a- ≥ 0 b b b t3 + 1− t2 − t ≥ 0.

Wielomian z lewej strony łatwo rozłożyć na czynniki.

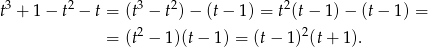
3 2 3 2 2 t + 1 − t − t = (t − t )− (t− 1 ) = t(t − 1) − (t− 1) = = (t2 − 1)(t − 1) = (t − 1)2(t+ 1).

Otrzymane wyrażenie jest oczywiście nieujemne.

Wersja PDF