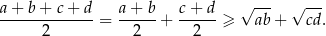/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 6086538

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 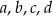a,b,c,d prawdziwa jest nierówność

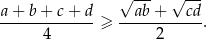
√ --- √ --- a+--b+--c+-d- ≥ --ab-+---cd-. 4 2

Rozwiązanie

Sposób I

Przekształcamy daną nierówność w sposób równoważny.

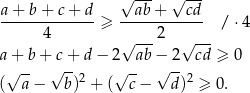
√ --- √ --- a+--b+--c+-d- ≥ --ab-+---cd- / ⋅4 4 √ ---2 √ --- a+ b+ c + d − 2 ab − 2 cd ≥ 0 √ -- √ -- √ - √ -- ( a− b)2 + ( c − d )2 ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy ją przy pomocy równoważności, więc wyjściowa nierówność również musiała być prawdziwa.

Sposób II

Zauważmy najpierw, że prawdziwa jest nierówność

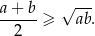
a-+-b- √ --- 2 ≥ ab.

Rzeczywiście, nierówność ta jest równoważna kolejno nierównościom

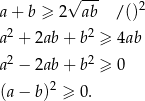
√ --- 2 a+ b ≥ 2 ab /() a2 + 2ab + b2 ≥ 4ab 2 2 a − 2ab + b ≥ 0 (a− b)2 ≥ 0.

Analogicznie uzasadniamy, że

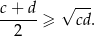
c+ d √ --- -----≥ cd. 2

Stąd

a+ b+ c + d a + b c + d √ --- √ --- -------------= ------+ ----- ≥ ab+ cd. 2 2 2
Wersja PDF