Zadanie nr 7345837
Udowodnij, że dla dowolnej dodatniej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
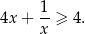
Rozwiązanie
Przekształcamy daną nierówność w sposób równoważny. Ponieważ 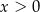 , możemy nierówność pomnożyć stronami przez
, możemy nierówność pomnożyć stronami przez  .
.
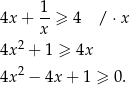
Prawdziwość otrzymanej nierówności uzasadnimy na dwa sposoby.
Sposób I
Zauważmy, że lewa strona nierówności to pełen kwadrat
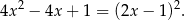
To oczywiście oznacza, że nierówność ta jest zawsze spełniona.
Sposób II
Wykresem lewej strony nierówności (traktowanej jako funkcja zmiennej  ) jest parabola o ramionach skierowanych w górę, której wierzchołek leży na osi
) jest parabola o ramionach skierowanych w górę, której wierzchołek leży na osi 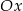 (bo
(bo 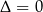 ). To oznacza, że nierówność ta rzeczywiście jest prawdziwa.
). To oznacza, że nierówność ta rzeczywiście jest prawdziwa.

