/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 7492422

Dodaj do ulubionych
Dodaj do rozwiązanych

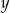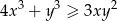Wykaż, że dla dowolnych nieujemnych liczb rzeczywistych x , y spełniona jest nierówność: 4x 3 + y 3 ≥ 3xy2 .

Rozwiązanie

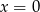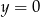Jeżeli x = 0 lub y = 0 to nierówność jest oczywiście spełniona, więc załóżmy, że x,y > 0 .

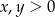Sposób I

Przekształcamy nierówność korzystając ze wzoru na sumę sześcianów.

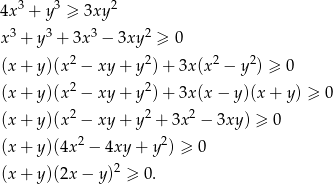
4x 3 + y 3 ≥ 3xy2 x3 + y3 + 3x 3 − 3xy 2 ≥ 0 2 2 2 2 (x + y)(x − xy + y )+ 3x(x − y ) ≥ 0 (x + y)(x 2 − xy + y2)+ 3x(x − y)(x + y) ≥ 0 (x + y)(x 2 − xy + y2 + 3x2 − 3xy) ≥ 0 2 2 (x + y)(4x − 4xy + y ) ≥ 0 (x + y)(2x − y)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.

Sposób II

Ponieważ nierówność jest jednorodna (każdy składnik jest jednomianem stopnia 3), możemy łatwo zamienić nierówność na nierówność, w której jest tylko jedna zmienna – dzielimy nierówność stronami przez 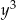y3 .

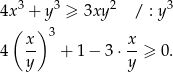
3 3 2 3 4x( +)y ≥ 3xy / : y x 3 x 4 -- + 1− 3 ⋅-- ≥ 0. y y

Podstawiamy teraz 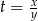x t = y i mamy

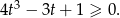
3 4t − 3t + 1 ≥ 0 .

Łatwo sprawdzić, że jednym z pierwiastków lewej strony jest 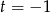t = − 1 , więc dzielimy ten wielomian przez t+ 1 .

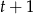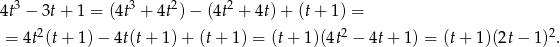
3 3 2 2 4t − 3t+ 1 = (4t + 4t ) − (4t + 4t)+ (t + 1) = = 4t2(t+ 1)− 4t(t + 1) + (t+ 1) = (t+ 1 )(4t2 − 4t + 1) = (t + 1)(2t− 1)2.

Teraz jest jasne, że dla 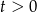t > 0 wielomian ten przyjmuje tylko wartości nieujemne.

Wersja PDF