Zadanie nr 7705704

Wykaż, że

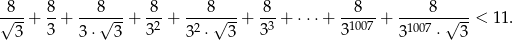
8 8 8 8 8 8 8 8 √---+ --+ ---√--+ -2-+ ----√---+ --3 + ⋅⋅⋅+ -1007-+ -------√---< 11 . 3 3 3⋅ 3 3 32 ⋅ 3 3 3 3 1007 ⋅ 3

Rozwiązanie

Zauważmy, że po lewej stronie nierówności mamy sumę 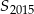S2015 początkowych wyrazów ciągu geometrycznego 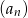(an) o ilorazie q = √13- :

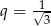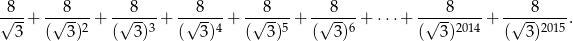
√8--+ -√-8---+ -√-8---+ -√-8---+ -√8---+ -√8---+ ⋅ ⋅⋅+ -√--8----+ -√--8----. 3 ( 3)2 ( 3)3 ( 3 )4 ( 3)5 ( 3)6 ( 3)2014 ( 3)2015

Sposób I

Suma wszystkich wyrazów nieskończonego ciągu 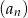(an) jest równa

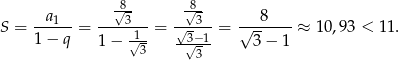
a √8- √8- 8 S = ---1--= ----3-- = -√-3--= √-------≈ 10,93 < 1 1. 1 − q 1 − √13 -3√−-1 3 − 1 3

To oczywiście oznacza, że suma częściowa 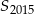S2015 jest jeszcze mniejsza.

Sposób II

Liczymy 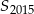S 2015 .

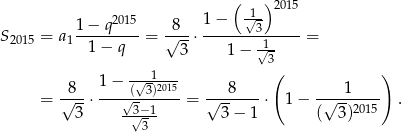
( )2015 1− q2015 8 1 − √13- S2015 = a1---------= √---⋅--------1-----= 1− q 3 1 − √3- ---1--- ( ) 8 1 − (√3)2015 8 1 = √---⋅---√-3−1----= √------⋅ 1− -√---2015- . 3 -√-3- 3− 1 ( 3)

Musimy zatem wykazać, że

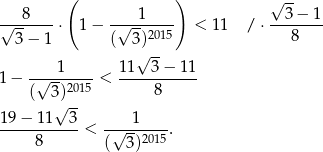
( ) √ -- 8 1 3− 1 √-------⋅ 1− -√---2015 < 11 /⋅ -------- 3 − 1 ( 3) 8 1 11 √ 3− 11 1− -√-------< ----------- ( 3)2015 8 19 − 11√ 3- 1 -----------< -√-------. 8 ( 3)2015

Ponieważ 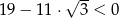√ -- 19 − 1 1⋅ 3 < 0 powyższa nierówność jest oczywiście spełniona, więc wyjściowa nierówność też musiała być prawdziwa.