/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 7903922

Dodaj do ulubionych
Dodaj do rozwiązanych

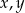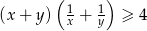Wykaż, że dla dowolnych dodatnich liczb rzeczywistych x,y prawdziwa jest nierówność ( ) (x + y) 1 + 1 ≥ 4 x y .

Rozwiązanie

Przekształcamy daną nierówność w sposób równoważny – liczby 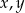x,y są dodatnie, więc możemy przez nie mnożyć nierówność stronami.

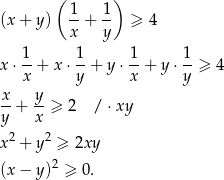
( ) (x+ y) 1-+ 1- ≥ 4 x y 1 1 1 1 x⋅ --+ x ⋅--+ y ⋅--+ y⋅ --≥ 4 x y x y x-+ y-≥ 2 / ⋅xy y x 2 2 x + y ≥ 2xy (x− y)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona.

Wersja PDF