/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 8126194

Dodaj do ulubionych
Dodaj do rozwiązanych

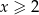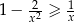Wykaż, że dla dowolnej liczby x ≥ 2 prawdziwa jest nierówność 2- 1 1 − x2 ≥ x .

Rozwiązanie

Przekształcamy daną nierówność w sposób równoważny. Ponieważ 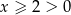x ≥ 2 > 0 , możemy obie strony pomnożyć przez x 2 .

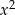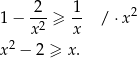
1 − 2--≥ 1- / ⋅x 2 x2 x x 2 − 2 ≥ x.

Sposób I

Korzystamy dwa razy z podanego założenia: 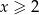x ≥ 2 .

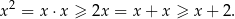
x2 = x ⋅x ≥ 2x = x + x ≥ x + 2 .

Sposób II

Rozwiązujemy otrzymaną nierówność kwadratową

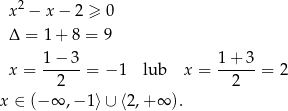
2 x − x − 2 ≥ 0 Δ = 1 + 8 = 9 1 − 3 1 + 3 x = ------= −1 lub x = ------= 2 2 2 x ∈ (− ∞ ,− 1⟩ ∪ ⟨2,+ ∞ ).

To pokazuje, że dana nierówność jest rzeczywiście prawdziwa dla 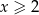x ≥ 2 .

Wersja PDF