Zadanie nr 8188153
Wykaż, że jeżeli 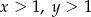 i
i 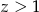 , to
, to 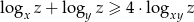 .
.
Rozwiązanie
Sposób I
Przekształcamy daną nierówność – zamieniamy podstawy wszystkich logarytmów na  . Po drodze będziemy korzystać z tego, że
. Po drodze będziemy korzystać z tego, że 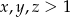 , co oznacza, że logarytmy z tych liczb są dodatnie.
, co oznacza, że logarytmy z tych liczb są dodatnie.
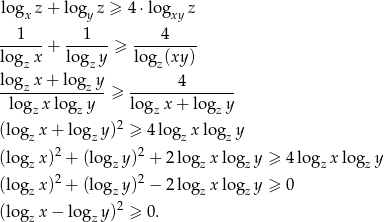
Otrzymana nierówność jest oczywiście prawdziwa, z przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.
Sposób II
Przekształcamy daną nierówność – zamieniamy wszystkie logarytmy na dziesiętne. Po drodze będziemy korzystać z tego, że 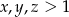 , co oznacza, że logarytmy z tych liczb są dodatnie.
, co oznacza, że logarytmy z tych liczb są dodatnie.
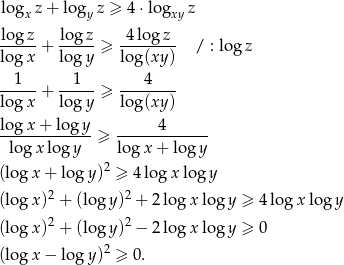
Otrzymana nierówność jest oczywiście prawdziwa, z przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.

