Zadanie nr 8195748
Wykaż, że jeżeli 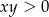 to
to 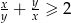 .
.
Rozwiązanie
Sposób I
Przekształcamy nierówność korzystając z podanego założenia.
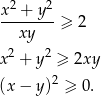
Otrzymana nierówność jest oczywiście prawdziwa.
Sposób II
Jeżeli iloczyn liczb  i
i 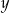 jest dodatni, to dodatni jest również ich iloraz. Więc nierówność jest równoważna nierówności
jest dodatni, to dodatni jest również ich iloraz. Więc nierówność jest równoważna nierówności
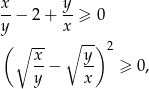
a ta nierówność jest oczywiście spełniona.

