Zadanie nr 9015821

Udowodnij, że dla dowolnego kąta 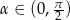π- α ∈ (0,2) prawdziwa jest nierówność

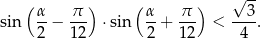
( ) ( ) √ -- sin α-− π-- ⋅sin α-+ π-- < --3. 2 12 2 12 4

Rozwiązanie

Sposób I

Korzystamy ze wzorów

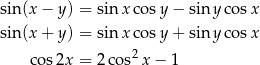
sin(x − y) = sin xco sy − siny cos x sin(x + y) = sin xco sy + siny cos x 2 co s2x = 2 cos x− 1

Mamy zatem

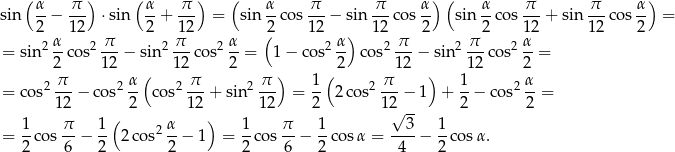
(α π ) (α π ) ( α π π α ) ( α π π α) sin --− --- ⋅sin --+ --- = sin --cos ---− sin---co s-- sin -co s---+ sin ---cos -- = 2 α 12 π 2 π12 α (2 12 α) 1 2 π 2 π 2 1α2 12 2 = sin2 -co s2---− sin2 ---cos2 --= 1− cos2 -- cos2 ---− sin2---co s2--= 2 12 ( 12 2 ) ( 2 12 ) 1 2 2 2 π-- 2 α- 2 π-- 2 π-- 1- 2 π-- 1- 2 α- = cos 12 − cos 2 cos 12 + sin 12 = 2 2 cos 12 − 1 + 2 − cos 2 = 1 π 1( α ) 1 π 1 √ 3- 1 = --cos --− -- 2co s2--− 1 = --co s--− --cosα = ----− --cos α. 2 6 2 2 2 6 2 4 2

Wystarczy teraz zauważyć, że z założenia 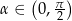( ) α ∈ 0, π2- , więc 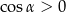cos α > 0 i

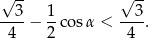
√ -- √ -- 3 1 3 ----− --cos α < ----. 4 2 4

Sposób II

Będziemy chcieli skorzystać ze wzoru

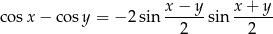
cos x− cosy = − 2sin x-−-y-sin x-+-y- 2 2

Na mocy tego wzoru

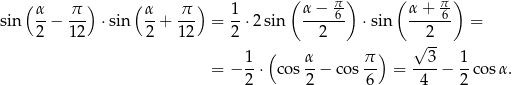
( ) ( ) ( π) ( π-) sin α-− -π- ⋅sin α-+ -π- = 1⋅ 2sin α-−--6 ⋅sin α-+--6 = 2 12 2 12 2 2 2 ( ) √ -- = − 1⋅ cos α-− cos π- = --3− 1-cosα . 2 2 6 4 2

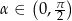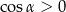Teraz wystarczy zauważyć, że z założenia ( ) α ∈ 0, π- 2 , więc cos α > 0 .