/Szkoła średnia/Nierówności/Udowodnij.../Z pierwiastkami

Zadanie nr 1660709

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnych różnych liczb rzeczywistych 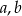a,b prawdziwa jest nierówność

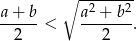
∘ -------- a+--b- a2 +-b2 2 < 2 .

Rozwiązanie

Jeżeli 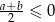a+b-- 2 ≤ 0 , to oczywiście nierówność jest spełniona, więc załóżmy, że 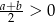a+b2-> 0 . Przy tym założeniu możemy nierówność podnieść stronami do kwadratu.

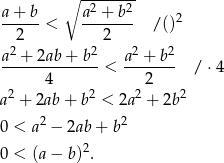
∘ -------- a+ b a2 + b2 ------< ------- / ()2 22 2 2 2 2 a-+--2ab-+-b-- a-+-b-- 4 < 2 / ⋅4 a2 + 2ab+ b2 < 2a2 + 2b2 0 < a2 − 2ab + b2 2 0 < (a − b) .

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy ją przy pomocy równoważności, więc wyjściowa nierówność również musiała być prawdziwa.

Wersja PDF