Zadanie nr 1907545
Udowodnij, że dla dowolnych liczb nieujemnych 
i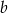 
prawdziwa jest nierówność
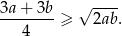
Rozwiązanie
Przekształcamy nierówność w sposób równoważny – obie strony są nieujemne, więc możemy nierówność podnieść stronami do kwadratu.
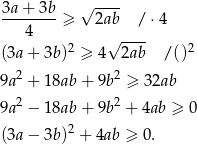
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być prawdziwa.
