Zadanie nr 4085373

Wykaż, że dla dowolnej liczby dodatniej prawdziwa jest nierówność

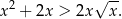
2 √ -- x + 2x > 2x x.

Rozwiązanie

Sposób I

Przekształcamy daną nierówność w sposób równoważny

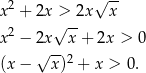
2 √ -- x + 2x√>-2x x x2 − 2x x + 2x > 0 √ --2 (x − x) + x > 0.

Teraz jest jasne, że nierówność ta jest zawsze spełniona (bo 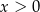x > 0 ).

Sposób II

Korzystamy z nierówności

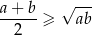
√ --- a+--b-≥ ab 2

między średnią arytmetyczną i geometryczną. Mamy zatem

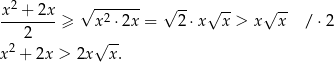
x2 + 2x √ ------- √ -- √ -- √ -- --------≥ x2 ⋅2x = 2 ⋅x x > x x / ⋅2 2 √ -- x2 + 2x > 2x x.

Po drodze skorzystaliśmy z tego, że 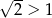√ -- 2 > 1 i x > 0 .

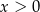Sposób III

Przekształcamy daną nierówność w sposób równoważny. Ponieważ 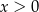x > 0 , możemy ją podzielić stronami przez .

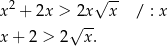
2 √ -- x + 2x > √2x- x / : x x + 2 > 2 x.

Obie strony są dodatnie, więc możemy nierówność podnieść stronami do kwadratu.

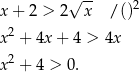
x + 2 > 2√x-- / ()2 x2 + 4x + 4 > 4x 2 x + 4 > 0.

Teraz jest jasne, że nierówność ta jest zawsze spełniona.

Sposób IV

Przekształcamy daną nierówność w sposób równoważny – obie strony są dodatnie, więc możemy nierówność podnieść stronami do kwadratu.

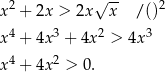
√ -- x 2 + 2x > 2x x / ()2 4 3 2 3 x + 4x + 4x > 4x x 4 + 4x2 > 0.

Teraz jest jasne, że nierówność ta jest zawsze spełniona.