/Szkoła średnia/Nierówności/Udowodnij.../Z pierwiastkami

Zadanie nr 4321609

Wykaż, że jeżeli 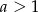a > 1 to prawdziwa jest nierówność

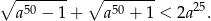
∘ -50---- ∘ -50---- 25 a − 1+ a + 1 < 2a .
Wersja PDF

Rozwiązanie

Obie strony są dodatnie, więc możemy nierówność podnieść stronami do kwadratu.

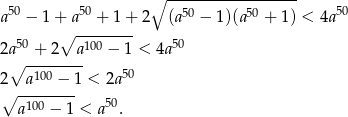
∘ ------------------ a50 − 1+ a50 + 1 + 2 (a50 − 1)(a50 + 1 ) < 4a50 ∘ -------- 2a50 + 2 a 100 − 1 < 4a 50 ∘ -------- 50 2 a100 − 1 < 2a ∘ --100---- 50 a − 1 < a .

Ponownie podnosimy obie strony do kwadratu.

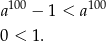
100 100 a − 1 < a 0 < 1.

Otrzymana nierówność jest oczywiście prawdziwa.

Wersja PDF