Zadanie nr 4844358

Wykaż, że dla każdej liczby 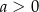a > 0 i dla każdej liczby 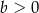b > 0 prawdziwa jest nierówność

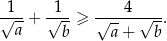
√1-+ √1--≥ √---4-√--. a b a+ b

Rozwiązanie

Sposób I

Przekształcamy nierówność.

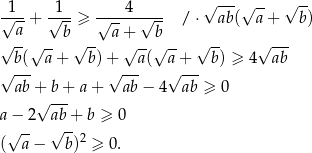
1 1 4 √ --- √ -- √ -- √--+ √---≥ √-----√--- / ⋅ ab ( a+ b) √ -a b√ -- a+ b √ -- √ --- b(√a--+ b )+ √a-(√a--+ b ) ≥ 4 ab √ --- √ --- √ --- ab + b + a + ab − 4 ab ≥ 0 √ --- a − 2 ab + b ≥ 0 √ -- √ --2 ( a − b) ≥ 0 .

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być spełniona.

Sposób II

Tak jak poprzednio dochodzimy do nierówności

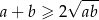
√ --- a + b ≥ 2 ab

Ponieważ obie strony tej nierówności są dodatnie, możemy podnieść ją stronami do kwadratu.

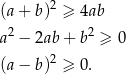
(a + b)2 ≥ 4ab 2 2 a − 2ab + b ≥ 0 (a − b)2 ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być spełniona.