/Szkoła średnia/Nierówności/Udowodnij.../Z pierwiastkami

Zadanie nr 6300958

Wykaż, że prawdziwa jest nierówność 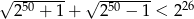√ -50---- √ -50---- 26 2 + 1+ 2 − 1 < 2 .

Wersja PDF

Rozwiązanie

Obie strony są dodatnie, więc możemy nierówność podnieść stronami do kwadratu.

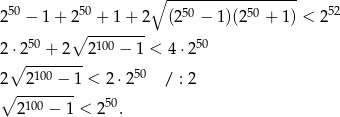
∘ ------------------ 250 − 1 + 250 + 1 + 2 (2 50 − 1)(250 + 1) < 2 52 ∘ -------- 2⋅2 50 + 2 2100 − 1 < 4⋅250 ∘ -------- 50 2 2100 − 1 < 2 ⋅2 / : 2 ∘ -100---- 50 2 − 1 < 2 .

Ponownie podnosimy obie strony do kwadratu.

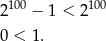
100 100 2 − 1 < 2 0 < 1.

Otrzymana nierówność jest oczywiście prawdziwa. Ponieważ przekształcenia były równoważnościami (możemy zapisać je od końca), dowodzi to prawdziwości wyjściowej nierówności.

Wersja PDF