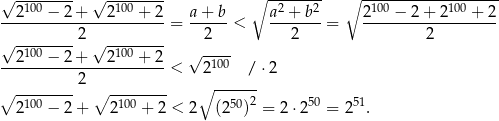/Szkoła średnia/Nierówności/Udowodnij.../Z pierwiastkami

Zadanie nr 8295787

  • Wykaż, że dla dowolnych różnych liczb dodatnich 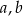a,b prawdziwa jest nierówność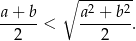
    ∘ -------- a + b a2 + b2 ------< -------. 2 2
  • Wykorzystując nierówność z punktu a), wykaż, że prawdziwa jest nierówność
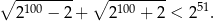
    ∘ -100---- ∘ -100---- 51 2 − 2+ 2 + 2 < 2 .
Wersja PDF

Rozwiązanie

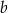  • Przekształcamy daną nierówność w sposób równoważny. Liczby a i b są dodatnie, więc możemy podnieść ją stronami do kwadratu.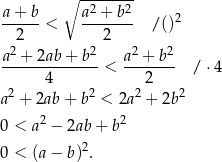
    ∘ -------- a + b a 2 + b2 ------< ------- /()2 2 2 a-2 +-2ab-+-b2 a2-+-b2 4 < 2 / ⋅4 2 2 2 2 a + 2ab + b < 2a + 2b 0 < a2 − 2ab + b2 2 0 < (a− b ) .

    Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność również musiała być prawdziwa.

  • W nierówności z poprzedniego podpunktu podstawiamy
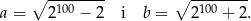
    ∘ -------- ∘ -------- a = 2100 − 2 i b = 2100 + 2.

    Mamy zatem

    √ --100---- √ -100---- ∘ --2---2- ∘ --100--------100---- --2----−-2-+---2---+--2 = a-+-b-< a--+-b- = 2----−-2-+-2---+--2 √ -------- 2 √ -------- 2 2 2 2 100 − 2 + 2100 + 2 √ ---- ----------------------- < 2100 / ⋅2 ∘ --------2 ∘ -------- ∘ ------ 2100 − 2 + 2 100 + 2 < 2 (250)2 = 2 ⋅250 = 251.
Wersja PDF