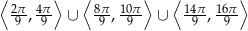/Szkoła średnia/Nierówności/Trygonometryczne/Rozwiąż nierówność

Zadanie nr 7496786

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 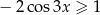− 2 cos3x ≥ 1 w przedziale ⟨0,2π ⟩ .

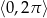Rozwiązanie

Daną nierówność możemy zapisać w postaci

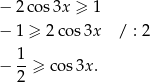
− 2 cos3x ≥ 1 − 1 ≥ 2 cos3x / : 2 1 − --≥ cos3x . 2

Szkicujemy cosinusa.

PIC

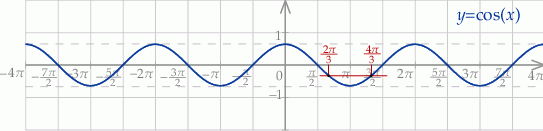
Rozwiązaniem powyższej nierówności jest

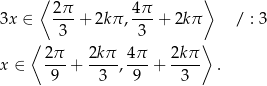
⟨ ⟩ 3x ∈ 2π-+ 2kπ , 4π-+ 2kπ / : 3 3 3 ⟨ 2π 2kπ 4π 2kπ ⟩ x ∈ ---+ ----,--- + ---- . 9 3 9 3

Teraz trzeba ustalić jaka część tego zbioru znajduje się w przedziale 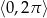⟨0,2π ⟩ . Łatwo zauważyć, że powyższe przedziały znajdują się w przedziale 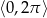⟨0,2π ⟩ tylko dla 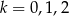k = 0,1,2 . Mamy więc rozwiązanie

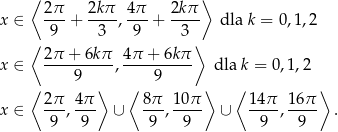
⟨ ⟩ 2π- 2kπ- 4π- 2kπ- x ∈ 9 + 3 , 9 + 3 dla k = 0,1,2 ⟨ ⟩ x ∈ 2π-+-6k-π-, 4π-+-6k-π dla k = 0,1,2 9 9 ⟨ 2π 4π ⟩ ⟨ 8π 10π ⟩ ⟨ 14π 1 6π ⟩ x ∈ ---,--- ∪ ---, ---- ∪ ----,---- . 9 9 9 9 9 9

 
Odpowiedź: ⟨ ⟩ ⟨ ⟩ ⟨ ⟩ 2π9 , 49π ∪ 89π, 109π ∪ 149π, 169π

Wersja PDF