/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z wykładniczą

Zadanie nr 2544139

Dodaj do ulubionych
Dodaj do rozwiązanych

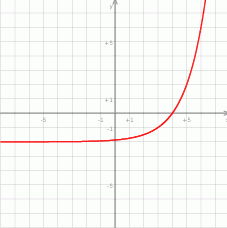
Na rysunku narysowano fragment wykresu funkcji 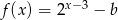x−3 f(x) = 2 − b , określonej dla x ∈ R .

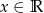  • Podaj wartość b .
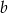  • Naszkicuj wykres funkcji g(x) = |f (x)| .
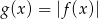  • Podaj wszystkie wartości parametru 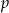p , dla których równanie 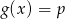g(x) = p ma dokładnie jedno rozwiązanie.
PIC

Rozwiązanie

  • Z wykresu widać, że miejscem zerowym funkcji jest 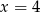x = 4 , więc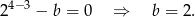
    4− 3 2 − b = 0 ⇒ b = 2.

     
    Odpowiedź: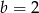 b = 2

  • Odbijamy kawałek poniżej osi 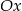Ox do góry.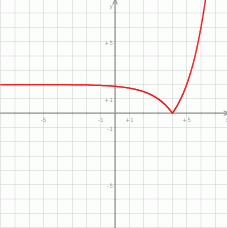
    PIC
  • Odczytujemy z wykresu w poprzednim podpunkcie:
    p ∈ {0} ∪ ⟨2,+ ∞ )

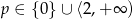
    (wykres przecina prostą 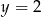y = 2 w jednym punkcie).  
    Odpowiedź: p ∈ {0} ∪ ⟨2,+ ∞ )

Wersja PDF