/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z wykładniczą

Zadanie nr 2686807

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji wykładniczej 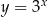x y = 3 przekształcono i otrzymano wykres funkcji 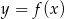y = f(x ) (rys).

PIC

Napisz wzór funkcji 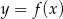y = f(x) , a następnie zaznacz na płaszczyźnie zbiór

{ } A = x,y : x ∈ R i y ∈ R i log(x−1)2+y 2[log 9f2(x)] < 0 .

Rozwiązanie

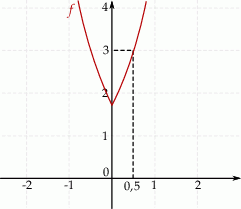
Wykres przedstawiony na rysunku powstaje z wykresu funkcji 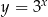x y = 3 przez przesunięcie o 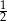12 w lewo, a potem odrzucenie części wykresu na lewo od osi 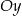Oy i odbiciu części znajdującej się na prawo od osi 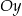Oy względem tej osi. Jest to więc funkcja

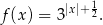
f(x) = 3|x|+12.

Spróbujmy teraz przekształcić interesującą nas nierówność.

log 2 2[log f2(x)] < 0 (x− 1)+y [ 9 ] ( |x|+ 12)2 log (x− 1)2+y 2 log9 3 < 0 [ 1] log (x− 1)2+y 2 log99 |x|+2 < 0 ( ) 1- log (x− 1)2+y 2 |x| + 2 < 0.

Mamy teraz dwie możliwości.
Jeżeli 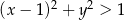(x − 1)2 + y2 > 1 to otrzymujemy nierówność

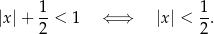
1 1 |x|+ 2-< 1 ⇐ ⇒ |x| < 2.

Jeżeli natomiast 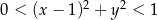0 < (x− 1)2 + y2 < 1 to mamy nierówność

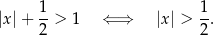
1 1 |x|+ --> 1 ⇐ ⇒ |x| > -. 2 2

Szkicujemy teraz ten zbiór.

PIC

 
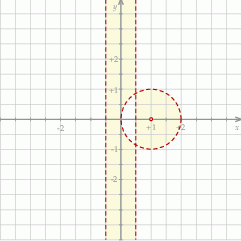
Odpowiedź: 1 f(x ) = 3|x|+ 2

Wersja PDF