/Szkoła średnia/Zadania maturalne/Matura 2012
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 31 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, którą spełnia liczba 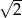 .
.
A) 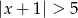 B)
B) 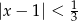 C)
C) 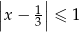 D)
D) 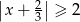
Liczba 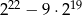 jest równa
jest równa
A) 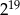 B)
B) 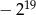 C)
C) 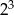 D)
D) 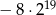
Ile rozwiązań posiada równanie: 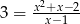 ?
?
A) 0 B) 1 C) 2 D) 3
Dane są wielomiany 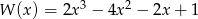 i
i 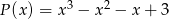 . Wielomian
. Wielomian 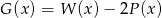 jest równy
jest równy
A) 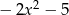 B)
B) 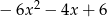 C)
C) 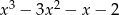 D)
D) 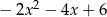
Do wykresu funkcji liniowej 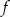 należą punkty
należą punkty 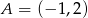 i
i 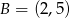 . Funkcja
. Funkcja 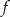 ma wzór
ma wzór
A) 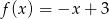 B)
B) 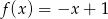 C)
C) 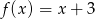 D)
D) 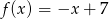
Do zbioru rozwiązań nierówności 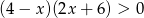 należy liczba
należy liczba
A) 3 B) 5 C) 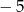 D)
D) 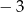
Kąt  jest ostry i
jest ostry i 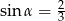 . Wartość wyrażenia
. Wartość wyrażenia 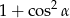 jest równa
jest równa
A) 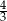 B)
B) 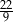 C)
C) 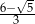 D)
D) 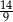
Podstawa 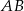 trójkąta
trójkąta 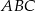 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 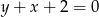 , a wierzchołek
, a wierzchołek 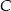 ma współrzędne
ma współrzędne 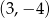 . Wysokość trójkąta opuszczona z wierzchołka
. Wysokość trójkąta opuszczona z wierzchołka 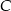 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 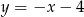 B)
B) 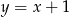 C)
C) 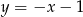 D)
D) 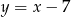
Różnica 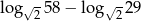 jest równa
jest równa
A) 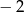 B)
B) 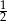 C) 2 D)
C) 2 D) 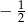
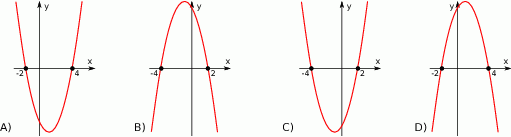
Dane są funkcje liniowe 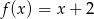 oraz
oraz 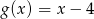 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 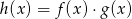 .
.
Dany jest nieskończony ciąg geometryczny 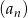 , w którym
, w którym 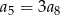 . Wtedy
. Wtedy
A) 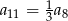 B)
B) 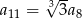 C)
C) 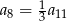 D)
D) 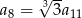
W ciągu arytmetycznym 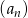 dane są
dane są 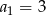 i
i 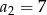 . Wtedy suma
. Wtedy suma 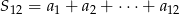 jest równa
jest równa
A) 324 B) 300 C) 282 D) 306
Ile jest liczb naturalnych trzycyfrowych o sumie cyfr równej 3?
A) 4 B) 5 C) 6 D) 7
Pole sześciokąta foremnego o boku długości 4 jest równe
A) 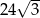 B)
B) 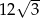 C)
C) 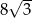 D)
D) 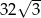
Stosunek boków prostokąta jest równy 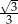 . Kąt ostry między przekątnymi prostokąta ma miarę
. Kąt ostry między przekątnymi prostokąta ma miarę
A) 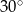 B)
B) 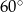 C)
C) 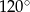 D)
D) 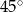
W trójkącie zwiększono długość każdego boku o 20%. O ile procent wzrosło pole tego trójkąta?
A) 20% B) 40% C) 44% D) 400%
Przekątna ściany sześcianu ma długość 10. Przekątna tego sześcianu ma długość
A) 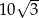 B)
B) 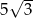 C)
C) 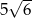 D)
D) 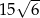
Prosta 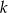 ma równanie
ma równanie 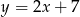 . Wskaż równanie prostej
. Wskaż równanie prostej 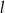 równoległej do prostej
równoległej do prostej 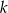 i przechodzącej przez punkt
i przechodzącej przez punkt 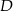 o współrzędnych
o współrzędnych 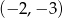 .
.
A) 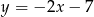 B)
B) 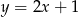 C)
C) 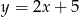 D)
D) 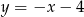
Obwód trójkąta 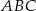 wynosi 28 cm, a jego pole jest równe
wynosi 28 cm, a jego pole jest równe 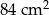 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 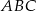 jest równy
jest równy
A) 3 cm B) 6 cm C) 4 cm D) 7 cm
Wskaż równanie okręgu o promieniu 9.
A) 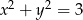 B)
B) 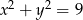 C)
C) 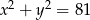 D)
D) 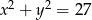
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 72. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 192 B) 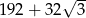 C)
C) 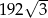 D)
D) 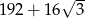
Punkty 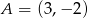 i
i 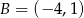 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 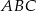 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 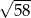 B)
B) 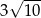 C)
C) 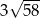 D)
D) 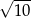
Prawdopodobieństwo zdarzenia 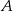 jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 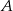 . Zatem
. Zatem 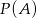 jest równe
jest równe
A) 0,6 B) 0,5 C) 0,4 D) 0,3
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 4 | 3 | 3 | 4 | 2 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
Zadania otwarte
Rozwiąż nierówność 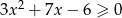 .
.
Ze zbioru liczb 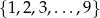 losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
Liczby 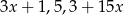 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
Wykaż, że jeśli 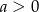 , to
, to 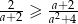 .
.
Przekątne czworokąta 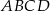 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 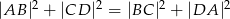 .
.
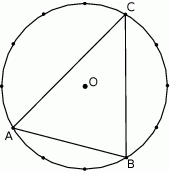
Punkty 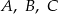 leżą na okręgu o środku
leżą na okręgu o środku 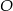 i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta
i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta 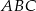 .
.
Okrąg o środku w punkcie 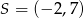 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 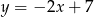 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Iloczyn cyfr liczby dwucyfrowej jest o 11 większy od sumy jej cyfr. Jeżeli przestawimy cyfry w tej liczbie, to otrzymamy liczbę o 36 większą od początkowej. Wyznacz tę liczbę.
Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 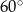 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 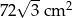 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.

