/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna
Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 7 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Liczbę 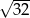 można przedstawić w postaci
można przedstawić w postaci
A) 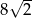 B)
B) 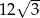 C)
C) 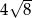 D)
D) 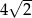
Potęga 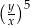 (gdzie
(gdzie  i
i 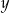 są różne od zera) jest równa
są różne od zera) jest równa
A) 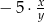 B)
B) 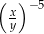 C)
C) 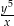 D)
D) 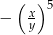
Liczba 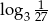 jest równa
jest równa
A) 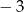 B)
B) 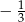 C)
C) 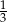 D) 3
D) 3
Wyrażenie 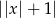 dla
dla 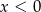 jest równe
jest równe
A) 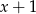 B)
B) 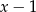 C)
C) 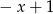 D)
D) 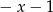
W pewnym sklepie ceny wszystkich płyt CD obniżono o 20%. Zatem za dwie płyty kupione w tym sklepie należy zapłacić mniej o
A) 10% B) 20% C) 30% D) 40%
Wielomian 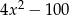 jest równy
jest równy
A) 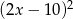 B)
B) 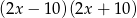 C)
C) 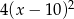 D)
D) 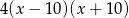
Równanie 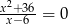
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Największą liczbą całkowitą spełniającą nierówność 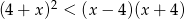 jest
jest
A) 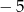 B)
B) 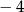 C)
C) 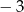 D)
D) 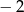
Funkcja liniowa 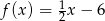
A) jest malejąca i jej wykres przechodzi przez punkt 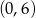
B) jest rosnąca i jej wykres przechodzi przez punkt 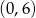
C) jest malejąca i jej wykres przechodzi przez punkt 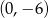
D) jest rosnąca i jej wykres przechodzi przez punkt 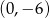
Liczby 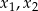 są rozwiązaniami równania
są rozwiązaniami równania 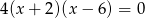 . Suma
. Suma 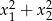 jest równa
jest równa
A) 16 B) 32 C) 40 D) 48
Na rysunku jest przedstawiony wykres funkcji 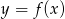 .
.
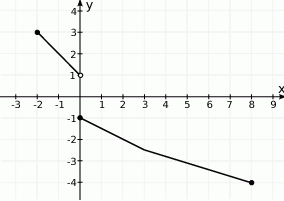
Zbiorem wartości tej funkcji jest
A) 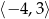 B)
B) 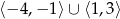 C)
C) 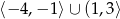 D)
D) 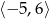
W trójkącie prostokątnym dane są kąty ostre: 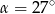 i
i 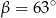 . Wtedy
. Wtedy 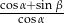 równa się
równa się
A) 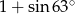 B)
B) 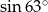 C) 1 D) 2
C) 1 D) 2
Ciąg arytmetyczny 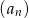 jest określony wzorem
jest określony wzorem 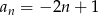 dla
dla 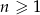 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 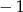 B) 1 C)
B) 1 C) 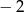 D) 3
D) 3
W ciągu geometrycznym 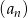 dane są
dane są 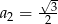 i
i 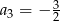 . Wtedy wyraz
. Wtedy wyraz 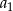 jest równy
jest równy
A) 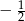 B)
B) 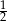 C)
C) 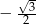 D)
D) 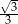
Dane są punkty 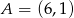 i
i 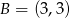 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 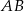 jest równy
jest równy
A) 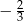 B)
B) 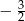 C)
C)  D)
D) 
Pole prostokąta jest równe 40. Stosunek długości jego boków jest równy 2:5. Dłuższy bok tego prostokąta jest równy
A) 10 B) 8 C) 7 D) 6
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Promień okręgu opisanego na tym trójkącie jest równy
A) 12 B) 8,5 C) 6,5 D) 5
Dane są dwa okręgi o promieniach 12 i 17. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych 13 i 15 wokół dłuższej przyprostokątnej. Promień podstawy tego stożka jest równy
A) 15 B) 13 C) 7,5 D) 6,5
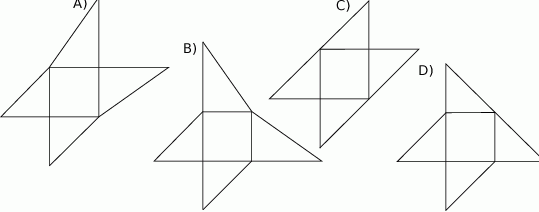
Dany jest sześcian 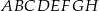 .
.
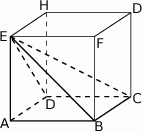
Siatką ostrosłupa czworokątnego 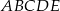 jest
jest
Jeżeli 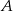 jest zdarzeniem losowym oraz
jest zdarzeniem losowym oraz 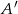 jest zdarzeniem przeciwnym do zdarzenia
jest zdarzeniem przeciwnym do zdarzenia 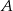 i
i 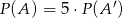 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 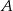 jest równe
jest równe
A) 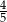 B)
B) 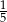 C)
C) 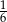 D)
D) 
Zadania otwarte
Rozwiąż nierówność 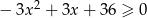 .
.
Funkcja 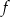 jest określona wzorem
jest określona wzorem 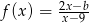 dla
dla 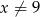 . Ponadto wiemy, że
. Ponadto wiemy, że 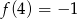 . Oblicz współczynnik
. Oblicz współczynnik 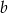 .
.
Podstawy trapezu prostokątnego mają długości 6 i 10 oraz tangens kąta ostrego jest równy 3. Oblicz pole tego trapezu.
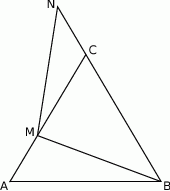
Trójkąt 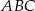 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 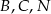 są współliniowe. Na boku
są współliniowe. Na boku 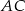 wybrano punkt
wybrano punkt 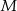 tak, że
tak, że 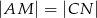 . Wykaż, że
. Wykaż, że 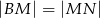 .
.
Liczby 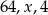 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 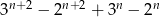 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III.
| Oceny | 6 | 5 | 4 | 3 | 2 | 1 |
| Liczba uczniów | 1 | 2 | 6 | 5 | 9 | 2 |
Oblicz średnią arytmetyczną i kwadrat odchylenia standardowego uzyskanych ocen.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 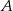 polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.
polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.
Podstawą ostrosłupa 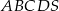 jest romb
jest romb 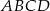 o boku długości 4. Kąt
o boku długości 4. Kąt 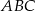 rombu ma miarę
rombu ma miarę 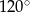 oraz
oraz 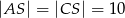 i
i 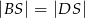 . Oblicz sinus kąta nachylenia krawędzi
. Oblicz sinus kąta nachylenia krawędzi 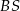 do płaszczyzny podstawy ostrosłupa.
do płaszczyzny podstawy ostrosłupa.
Wyznacz równanie okręgu przechodzącego przez punkt 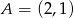 i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Z dwóch miast 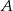 i
i 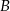 , odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta
, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta 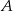 o jedną godzinę wcześniej niż drugi z miasta
o jedną godzinę wcześniej niż drugi z miasta 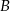 . Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta
. Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta 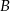 jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta
jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta 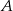 .
.

