/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 24 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Liczba 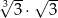 jest równa
jest równa
A) 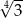 B)
B) 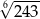 C)
C) 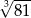 D)
D) 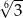
Rozwiązanie równania 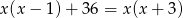 należy do przedziału
należy do przedziału
A) 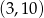 B)
B) 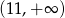 C)
C) 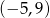 D)
D) 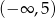
Liczba 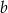 stanowi 40% liczby
stanowi 40% liczby  . O ile procent liczba
. O ile procent liczba  jest większa od liczby
jest większa od liczby 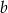 ?
?
A) 25% B) 60% C) 250% D) 150%
Funkcja 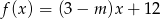 jest malejąca, gdy
jest malejąca, gdy
A) 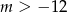 B)
B) 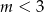 C)
C) 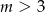 D)
D) 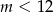
Układ równań 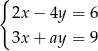 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 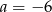 B)
B) 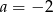 C)
C) 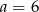 D)
D) 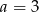
Przez jakie wyrażenie należy przemnożyć sumę 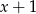 , aby otrzymać sumę
, aby otrzymać sumę 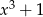 ?
?
A) 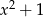 B)
B) 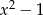 C)
C) 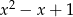 D)
D) 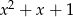
Jeżeli 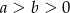 to wyrażenie
to wyrażenie 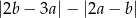 jest równe
jest równe
A) 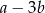 B)
B) 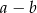 C)
C) 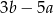 D)
D) 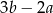
Jeżeli 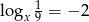 to liczba
to liczba  jest równa
jest równa
A) 3 B) 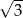 C)
C) 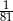 D) 81
D) 81
Zbiorem rozwiązań nierówności 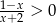 jest
jest
A) 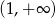 B)
B) 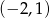 C)
C) 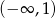 D)
D) 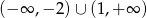
Wierzchołek paraboli 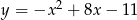 leży na prostej o równaniu
leży na prostej o równaniu
A) 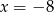 B)
B) 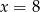 C)
C) 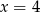 D)
D) 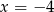
Na rysunku 1 jest przedstawiony wykres funkcji 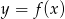 .
.
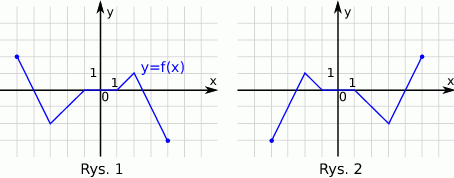
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 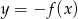 B)
B) 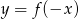 C)
C) 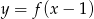 D)
D) 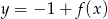
W ciągu geometrycznym 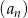 mamy
mamy 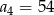 i
i 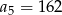 . Wtedy wyraz
. Wtedy wyraz 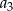 jest równy
jest równy
A) 6 B) 18 C) 2 D) 27
Kąt  jest ostry i
jest ostry i 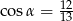 . Wtedy
. Wtedy
A) 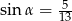 oraz
oraz 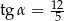
B) 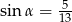 oraz
oraz 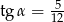
C) 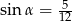 oraz
oraz 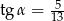
D) 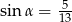 oraz
oraz 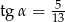
Promień okręgu opisanego na trójkącie równobocznym ma długość 4. Zatem bok tego trójkąta ma długość
A) 12 B) 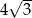 C) 4 D)
C) 4 D) 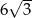
Suma wszystkich dwucyfrowych liczb parzystych jest równa
A) 2376 B) 2484 C) 2332 D) 2430
Ciąg 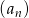 określony jest wzorem
określony jest wzorem 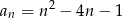 , gdzie
, gdzie 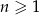 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 5
Punkt 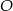 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
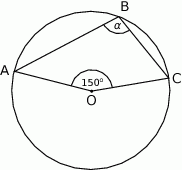
A) 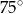 B)
B) 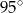 C)
C) 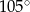 D)
D) 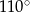
Przekrój osiowy walca jest kwadratem o polu 8. Pole powierzchni całkowitej tego walca jest równe
A) 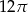 B)
B) 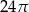 C)
C) 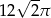 D)
D) 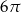
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej cztery wynosi
A) 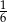 B)
B) 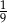 C)
C) 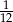 D)
D) 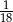
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 5 | 3 | 4 | 1 | 5 | 2 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 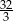 B) 3,5 C) 3,2 D)
B) 3,5 C) 3,2 D) 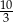
Znajdź skalę podobieństwa trójkąta 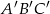 do trójkąta
do trójkąta 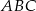 :
:
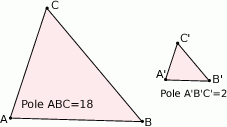
A) 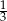 B)
B) 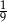 C) 3 D) 9
C) 3 D) 9
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 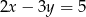 jest równy
jest równy
A) 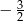 B)
B)  C)
C)  D) 2
D) 2
Zadania otwarte
Rozwiąż nierówność 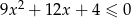 .
.
Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 21, czyli 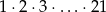 , jest podzielny przez
, jest podzielny przez 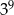 .
.
Liczby 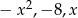 w podanej kolejności tworzą ciąg geometryczny. Oblicz
w podanej kolejności tworzą ciąg geometryczny. Oblicz  .
.
Rozwiąż równanie 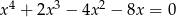 .
.
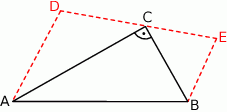
Na przyprostokątnych 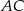 i
i 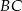 trójkąta prostokątnego
trójkąta prostokątnego 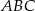 zbudowano trójkąty równoramienne
zbudowano trójkąty równoramienne 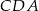 i
i 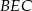 w ten sposób, że
w ten sposób, że 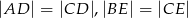 oraz punkty
oraz punkty 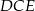 leżą na jednej prostej. Wykaż, że proste
leżą na jednej prostej. Wykaż, że proste 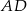 i
i 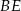 są równoległe.
są równoległe.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz pole tego trapezu.
Napisz równanie symetralnej boku 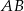 trójkąta
trójkąta 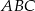 o wierzchołkach
o wierzchołkach 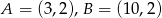 i
i 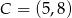 .
.
Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
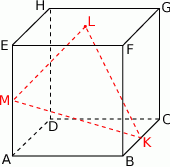
Punkty 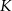 i
i 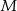 są środkami krawędzi
są środkami krawędzi 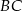 i
i 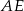 sześcianu
sześcianu 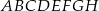 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 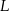 jest środkiem ściany
jest środkiem ściany 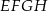 (zobacz rysunek). Oblicz obwód trójkąta
(zobacz rysunek). Oblicz obwód trójkąta 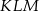 .
.
Pierwsza pompa napełnia zbiornik w czasie o 15 godzin krótszym niż druga pompa. Jeżeli obie pompy pracują jednocześnie, to zbiornik zostaje napełniony w czasie 10 godzin. Ile godzin potrzeba na napełnienie zbiornika przy pomocy każdej z pomp?

