/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna
Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom podstawowy 15 luty 2012 Czas pracy: 170 minut
Zadania zamknięte
Liczba 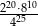 jest równa
jest równa
A) 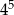 B)
B) 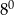 C)
C) 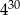 D)
D) 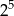
Liczba 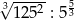 jest równa
jest równa
A) 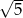 B)
B) 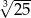 C)
C) 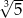 D) 5
D) 5
Liczbą przeciwną do liczby 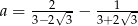 jest liczba
jest liczba
A) 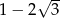 B)
B) 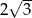 C)
C) 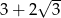 D)
D) 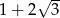
Liczba  stanowi 20% liczby
stanowi 20% liczby 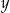 . Zatem prawdziwe jest następujące równanie
. Zatem prawdziwe jest następujące równanie
A) 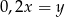 B)
B) 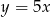 C)
C) 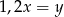 D)
D) 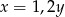
Wartość liczbowa wyrażenia 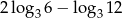 jest równa
jest równa
A) 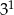 B)
B) 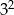 C)
C) 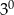 D)
D) 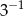
Ile rozwiązań ma układ równań 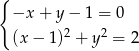 ?
?
A) 0 B) 1 C) 2 D) 3
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 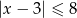 B)
B) 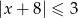 C)
C) 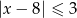 D)
D) 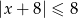
Zbiorem wartości funkcji 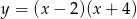 jest przedział
jest przedział
A) 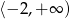 B)
B) 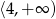 C)
C) 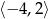 D)
D) 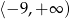
Odcinek o długości 60 cm podzielono na trzy części, których stosunek długości jest równy 3:4:5. Najdłuższa z tych części ma długość
A) 30 cm B) 12,5 cm C) 25 cm D) 15 cm
Prosta 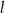 ma równanie
ma równanie 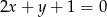 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do 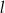 .
.
A) 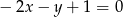 B)
B) 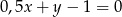 C)
C) 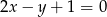 D)
D) 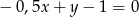
Rozwiązaniem równania 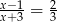 jest liczba
jest liczba
A) 1 B) 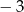 C) 9 D)
C) 9 D) 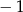
Do okręgu o równaniu 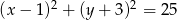 należy punkt
należy punkt
A) 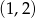 B)
B) 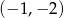 C)
C) 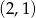 D)
D) 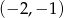
Wskaż przedział, który jest zbiorem rozwiązań nierówności 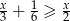
A) 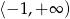 B)
B) 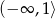 C)
C) 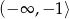 D)
D) 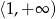
Liczba 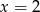 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 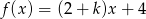 dla
dla
A) 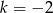 B)
B) 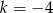 C)
C) 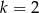 D)
D) 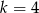
Największa wartość funkcji 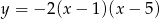 wynosi
wynosi
A) 2 B) 5 C) 8 D) 1
Boki równoległoboku mają długość 8 cm i 10 cm, a jego pole wynosi 40 cm. Kąt ostry równoległoboku ma miarę:
A) 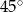 B)
B) 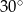 C)
C) 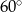 D)
D) 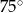
Ile wynosi suma dwunastu początkowych wyrazów nieskończonego ciągu arytmetycznego 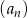 , w którym
, w którym 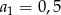 oraz różnica
oraz różnica 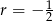 ?
?
A) 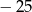 B)
B) 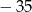 C)
C) 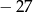 D)
D) 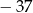
Odchylenie standardowe zestawu danych: 1, 2, 3, 4, 5 jest równe
A) 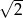 B) 2 C)
B) 2 C) 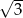 D) 3
D) 3
W ciągu geometrycznym 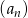 , gdzie
, gdzie 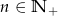 dane są:
dane są: 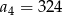 i
i 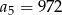 . Zatem:
. Zatem:
A) 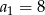 B)
B) 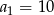 C)
C) 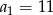 D)
D) 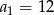
Wyrażenie 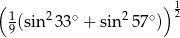 jest równe
jest równe
A) 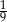 B)
B) 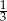 C) 1 D)
C) 1 D) 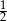
Funkcja
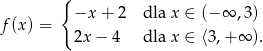
A) nie ma miejsc zerowych
B) ma dwa miejsca zerowe
C) ma jedno miejsce zerowe
D) ma trzy miejsca zerowe
Stosunek pola koła wpisanego w kwadrat do pola koła opisanego na tym kwadracie jest równy:
A) 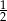 B)
B) 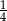 C)
C) 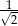 D)
D) 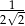
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano kartę pikową lub waleta?
A) 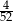 B)
B) 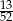 C)
C) 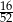 D)
D) 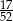
Zadania otwarte
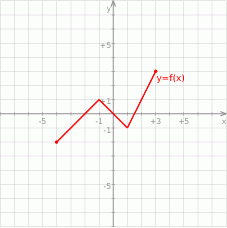
Na rysunku przedstawiony jest wykres funkcji 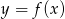 . Dla jakich argumentów funkcja
. Dla jakich argumentów funkcja 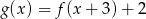 jest rosnąca?
jest rosnąca?
Rozwiąż równanie 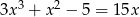 .
.
Dany jest trójkąt ostrokątny równoramienny 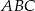 , w którym bok
, w którym bok 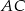 jest równy
jest równy 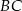 . Odcinek
. Odcinek 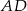 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 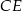 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 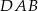 jest równy kątowi
jest równy kątowi 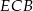 .
.
Uzasadnij, że dana równość 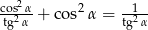 jest prawdziwa.
jest prawdziwa.
Oblicz  , jeśli
, jeśli 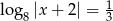 .
.
Wiesz, że funkcja kwadratowa 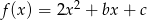 przyjmuje wartość najmniejszą
przyjmuje wartość najmniejszą 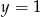 dla
dla 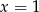 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 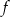 , a następnie rozwiąż równanie
, a następnie rozwiąż równanie 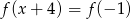 .
.
Dana jest funkcja 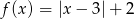 dla
dla 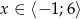 .
.
- zapisz wzór tej funkcji opuszczając symbol wartości bezwzględnej,
- naszkicuj wykres funkcji
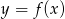 ,
, - naszkicuj wykres funkcji
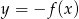 .
.
Statek płynący z prędkością własną 25 km/h, przepływa odległość z portu 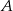 do
do 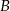 z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami
z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami 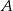 i
i 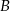 .
.
W graniastosłupie prostym o podstawie rombu krótsza przekątna podstawy ma długość 6 cm i tworzy z krawędzią podstawy kąt 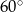 . Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę
. Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 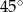 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.

