/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna

Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 5 marca 2012 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

W jednokładności o środku 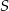S i skali 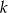k obrazem okręgu o równaniu 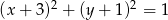(x+ 3)2 + (y+ 1)2 = 1 jest okrąg o równaniu 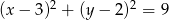(x − 3)2 + (y− 2)2 = 9 . Oblicz współrzędne środka 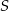S jednokładności.

Zadanie 2
(4 pkt)

Dla jakich wartości parametru α suma kwadratów różnych pierwiastków równania

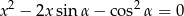
x 2 − 2x sinα − c os2α = 0

jest równa 3?

Zadanie 3
(4 pkt)

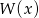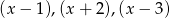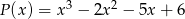Wielomian W (x) przy dzieleniu przez dwumiany (x − 1),(x + 2),(x − 3 ) daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 3 2 P (x) = x − 2x − 5x + 6 .

Zadanie 4
(4 pkt)

Narysuj wykres funkcji 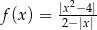|x2− 4| f (x) = -2−-|x|- , a następnie określ, dla jakich wartości parametru 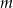m równanie 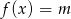f (x) = m nie ma rozwiązania.

Zadanie 5
(5 pkt)

W ciągu arytmetycznym wyraz pierwszy jest równy 1, a ostatni 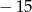− 15 . Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.

Zadanie 6
(4 pkt)

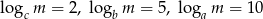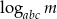Wiedząc, że lo gcm = 2, lo gb m = 5, logam = 1 0 oblicz lo gabc m .

Zadanie 7
(5 pkt)

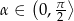Graniastosłup prawidłowy czworokątny o krawędzi podstawy równej a i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary ( ⟩ α ∈ 0, π 2 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.

Zadanie 8
(4 pkt)

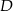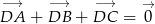Udowodnij, że jeżeli punkt D jest środkiem ciężkości trójkąta, to − → −→ −→ → DA + DB + DC = 0 .

Zadanie 9
(4 pkt)

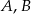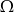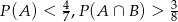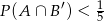Wykaż, że jeżeli A,B są podzbiorami Ω oraz P(A ) < 47 ,P (A ∩ B ) > 38 , to P (A ∩ B ′) < 15 .

Zadanie 10
(4 pkt)

Rozwiąż równanie 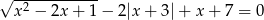√ ------------ x 2 − 2x + 1− 2 |x + 3 |+ x + 7 = 0 .

Zadanie 11
(4 pkt)

Na czworokącie wypukłym 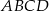ABCD można opisać okrąg. Wiadomo, że 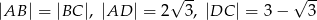√ -- √ -- |AB | = |BC |, |AD | = 2 3, |DC | = 3− 3 oraz przekątna 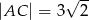√ -- |AC | = 3 2 . Oblicz pole tego czworokąta.

Zadanie 12
(3 pkt)

Przedstaw wielomian 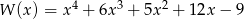4 3 2 W (x) = x + 6x + 5x + 12x − 9 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.

Arkusz Wersja PDF
Rozwiązania