/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony 11 stycznia 2012 Czas pracy: 180 minut
Jednym z pierwiastków wielomianu 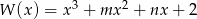 jest liczba 1. Reszta z dzielenia wielomianu
jest liczba 1. Reszta z dzielenia wielomianu 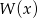 przez dwumian
przez dwumian 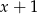 jest równa 4. Oblicz współczynniki
jest równa 4. Oblicz współczynniki 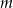 i
i  .
.
Rozwiąż równanie 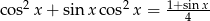 w przedziale
w przedziale 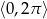 .
.
Uzasadnij, że 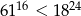 .
.
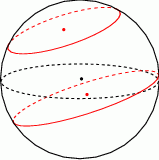
Kulę o promieniu 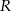 przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie
przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie 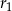 oraz
oraz 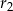 i są odległe od siebie o
i są odległe od siebie o  . Liczby
. Liczby 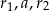 w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.
w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.
Rozwiąż nierówność 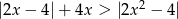 .
.
Wyznacz wszystkie wartości parametru 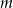 , dla których jedno rozwiązanie równania
, dla których jedno rozwiązanie równania
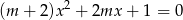
jest sinusem, a drugie cosinusem tego samego kąta?
W układzie współrzędnych przedstawiony jest wykres funkcji 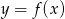 , gdzie
, gdzie 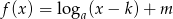 . Wyznacz wartości
. Wyznacz wartości 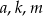 .
.
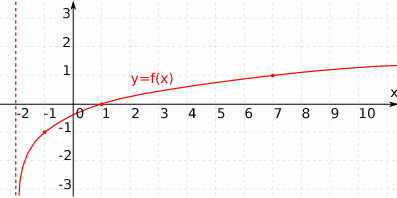
Pole trójkąta 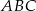 o danych wierzchołkach
o danych wierzchołkach 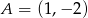 oraz
oraz 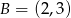 jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu
jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu 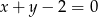 .
.
Na bokach 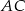 i
i 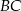 trójkąta
trójkąta 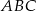 obrano punkty
obrano punkty 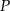 i
i 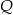 takie, że
takie, że 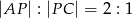 oraz
oraz 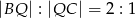 . Odcinki
. Odcinki 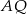 i
i 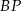 przecinają się w punkcie
przecinają się w punkcie 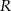 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 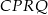 jest równe polu trójkąta
jest równe polu trójkąta 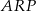 .
.
W graniastosłupie prawidłowym czworokątnym przekątne ścian bocznych, wychodzące z tego samego wierzchołka, mają długość 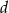 i tworzą kąt o mierze
i tworzą kąt o mierze  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.

