/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy 11 stycznia 2012 Czas pracy: 170 minut
Zadania zamknięte
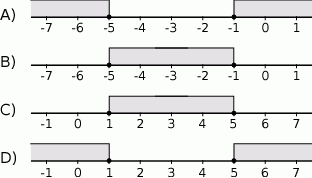
Zbiór rozwiązań nierówności 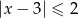 przedstawiony jest na osi liczbowej:
przedstawiony jest na osi liczbowej:
Jeżeli liczbę 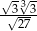 zapiszemy w postaci
zapiszemy w postaci 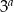 , to
, to  jest równe
jest równe
A) 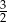 B)
B) 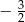 C)
C) 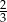 D)
D) 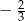
Jeżeli 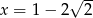 i
i 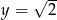 , to
, to 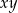 równe jest
równe jest
A) 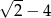 B)
B) 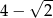 C)
C) 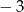 D)
D) 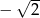
Liczba 3 nie należy do dziedziny wyrażenia
A) 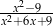 B)
B) 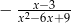 C)
C) 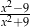 D)
D) 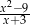
Rozwiązaniem nierówności 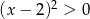 jest
jest
A) 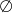 B) 2 C)
B) 2 C) 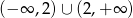 D)
D) 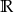
Rozwiązaniem równania 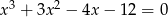 nie jest liczba
nie jest liczba
A) 2 B) 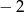 C)
C) 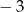 D) 3
D) 3
Funkcja określona wzorem
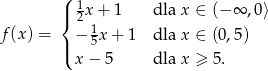
A) nie ma miejsc zerowych
B) ma 1 miejsce zerowe
C) ma 2 miejsca zerowe
D) ma 3 miejsc zerowe
Najmniejsza wartość funkcji 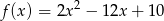 w przedziale
w przedziale 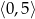 jest równa
jest równa
A) -1 B) -8 C) -10 D) 0
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 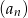 wyraża się wzorem
wyraża się wzorem 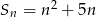 (
(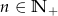 ). Drugi wyraz ciągu
). Drugi wyraz ciągu 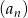 jest równy
jest równy
A) 2 B) 8 C) 12 D) 14
Dany jest ciąg geometryczny 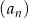 , w którym
, w którym 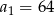 i
i 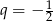 . Wówczas
. Wówczas
A) 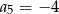 B)
B) 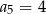 C)
C) 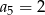 D)
D) 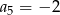
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 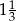 C)
C)  D)
D) 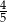
Rozwiązanie równania 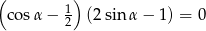 w przedziale
w przedziale 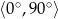 , to
, to
A) 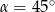 lub
lub 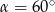
B) 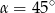 lub
lub 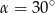
C) 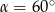 lub
lub 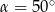
D) 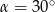 lub
lub 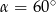
Miara kąta  , zaznaczonego na rysunku, jest równa
, zaznaczonego na rysunku, jest równa
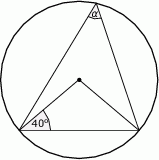
A) 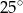 B)
B) 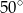 C)
C) 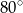 D)
D) 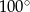
Suma miar kąta wpisanego i kąta środkowego, opartych na  okręgu, jest równa
okręgu, jest równa
A) 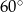 B)
B) 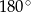 C)
C) 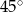 D)
D) 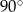
Punkty 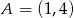 i
i 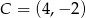 wyznaczają przekątną kwadratu
wyznaczają przekątną kwadratu 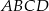 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 45 B) 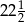 C) 18 D)
C) 18 D) 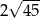
Proste 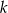 i
i 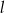 są równoległe. Odcinek
są równoległe. Odcinek  ma długość
ma długość
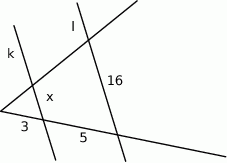
A) 9,6 B) 2 C) 6 D) 1,5
Promień okręgu o równaniu 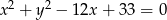 ma długość
ma długość
A) 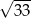 B)
B) 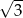 C) 3 D) 6
C) 3 D) 6
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 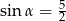 B)
B) 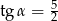 C)
C) 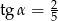 D)
D) 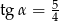
Objętość kuli wpisanej w sześcian o krawędzi długości 2 jest równa
A) 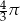 B)
B) 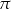 C)
C) 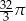 D)
D) 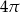
Dany jest przedział liczbowy 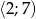 . Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
. Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
A) 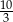 B)
B) 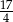 C) 4 D) 5
C) 4 D) 5
Dla zestawu liczb: 1, 3, 2, 4, 3
A) mediana jest równa 2 i średnia arytmetyczna jest równa 2,6.
B) mediana jest równa 3 i średnia arytmetyczna jest równa 3.
C) mediana jest równa 2 i średnia arytmetyczna jest równa 3.
D) mediana jest równa 3 i średnia arytmetyczna jest równa 2,6.
W pudełku znajduje się 5 kartek, na których zapisano wszystkie możliwe jednocyfrowe liczby naturalne nieparzyste. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 120 B) 125 C) 60 D) 15
Liczb trzycyfrowych o jednakowej cyfrze setek i jedności jest
A) 900 B) 90 C) 100 D) 300
Zadania otwarte
Rozwiąż równanie 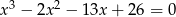 .
.
Udowodnij, że suma kwadratów dwóch kolejnych liczb nieparzystych jest liczbą parzystą.
Wyznacz sumę wszystkich dwucyfrowych parzystych liczb naturalnych.
Wyznacz miarę kąta ostrego  , dla którego wyrażenie
, dla którego wyrażenie 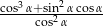 ma wartość 2.
ma wartość 2.
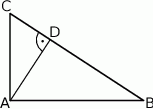
Trójkąt 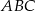 jest prostokątny. Punkt
jest prostokątny. Punkt 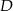 jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 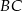 oraz
oraz 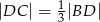 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 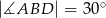 .
.
Wyznacz równania stycznych do okręgu o równaniu 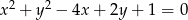 , równoległych do osi odciętych układu współrzędnych.
, równoległych do osi odciętych układu współrzędnych.
Wśród 150 mieszkańców pewnego osiedla przeprowadzono ankietę. Zadano pytanie, z jakiej sieci telefonii komórkowej korzystają. Wyniki badania przedstawiono w tabeli:
| Sieć | Ile osób korzysta |
| „Krzyżyk” | 75 |
| „Kółko” | 60 |
Okazało się, że wśród ankietowanych, 10 osób posiada telefony w obydwu sieciach. Oblicz prawdopodobieństwo, że losowo wybrana osoba spośród ankietowanych nie posiada telefonu w żadnej z wymienionych sieci. Wynik przedstaw w formie nieskracalnego ułamka.
Liczba  jest o 3 większa od liczby
jest o 3 większa od liczby 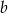 . Iloraz liczb
. Iloraz liczb  i
i 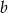 jest dwa razy mniejszy od sumy tych liczb. Wyznacz liczby
jest dwa razy mniejszy od sumy tych liczb. Wyznacz liczby  i
i 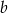 .
.
Mamy dwa pojemniki: pierwszy ma kształt sześcianu, drugi - ostrosłupa prawidłowego czworokątnego. Przekątna sześcianu ma długość 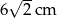 . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze
. Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 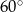 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 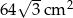 . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.
. Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.

