/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 2 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
Liczba  stanowi 60% liczby
stanowi 60% liczby 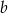 . Wówczas:
. Wówczas:
A) 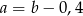 B)
B) 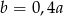 C)
C) 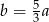 D)
D) 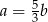
Dziedziną funkcji 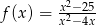 jest zbiór
jest zbiór
A) 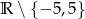 B)
B) 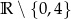 C)
C) 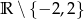 D)
D) 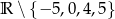
Ilustracją graficzną zbioru rozwiązań nierówności 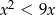 jest przedział:
jest przedział:

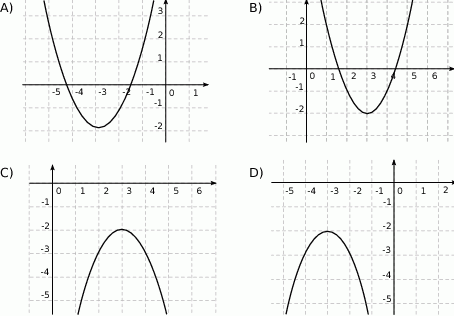
Wykresem funkcji 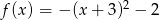 jest:
jest:
Osiemnasty wyraz ciągu arytmetycznego 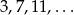 jest równy:
jest równy:
A) 71 B) 68 C) 75 D) 72
Kąt  jest ostry i
jest ostry i 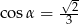 . Wtedy:
. Wtedy:
A) 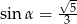 B)
B) 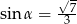 C)
C) 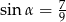 D)
D) 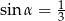
Odległość środka okręgu od prostej jest równa 0. Zatem liczba punktów wspólnych okręgu i prostej jest równa:
A) 0 B) 1 C) 2 D) 3
Prosta prostopadła do prostej 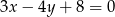 ma równanie:
ma równanie:
A) 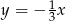 B)
B) 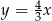 C)
C) 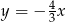 D)
D) 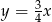
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) dziesięciokąt D) dwunastokąt
Średnia arytmetyczna liczb 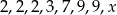 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 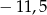 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Jeżeli 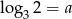 , to liczba
, to liczba 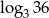 jest równa
jest równa
A) 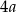 B)
B) 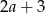 C)
C) 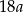 D)
D) 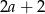
Dla 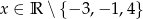 wyrażenie
wyrażenie 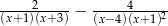 po sprowadzeniu do wspólnego mianownika ma postać
po sprowadzeniu do wspólnego mianownika ma postać
A) 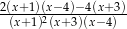 B)
B) 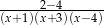 C)
C) 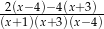 D)
D) 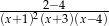
Pole trójkąta, w którym wysokość jest o 3 cm dłuższa od podstawy jest równe 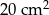 Wysokość trójkąta jest równa:
Wysokość trójkąta jest równa:
A) 5 cm B) 8 cm C) 2 cm D) 11 cm
Najmniejsza wartość funkcji 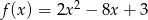 w przedziale
w przedziale 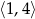 jest równa:
jest równa:
A) 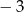 B) 5 C)
B) 5 C) 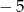 D)
D) 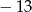
Pan Jan spłacał kredyt w wysokości 15 000 zł w sześciu ratach, z których każda kolejna była o 500 zł mniejsza od poprzedniej. Pierwsza rata była równa:
A) 2 500 zł B) 3 750 zł C) 7 500 zł D) 3 250 zł
Wiadomo, że 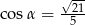 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia 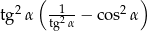 jest równa:
jest równa:
A) 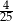 B)
B) 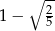 C)
C) 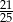 D)
D) 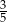
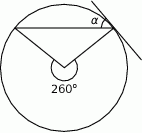
Prosta jest styczna do okręgu. Kąt  (patrz rysunek) ma miarę:
(patrz rysunek) ma miarę:
A) 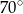 B)
B) 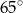 C)
C) 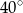 D)
D) 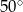
Środek okręgu o równaniu 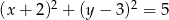 ma współrzędne:
ma współrzędne:
A) 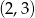 B)
B) 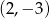 C)
C) 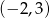 D)
D) 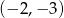
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 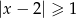 B)
B) 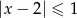 C)
C) 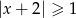 D)
D) 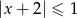
Wartość wyrażenia 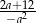 dla
dla 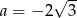 jest równa
jest równa
A) 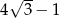 B)
B) 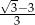 C)
C) 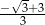 D)
D) 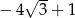
Liczba miejsc zerowych funkcji
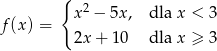
jest równa
A) 0 B) 1 C) 2 D) 3
Ze zbioru 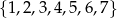 wybieramy kolejno cztery liczby bez zwracania i układamy je w kolejności losowania w liczbę czterocyfrową. Liczb czterocyfrowych podzielnych przez 5 otrzymamy:
wybieramy kolejno cztery liczby bez zwracania i układamy je w kolejności losowania w liczbę czterocyfrową. Liczb czterocyfrowych podzielnych przez 5 otrzymamy:
A) 216 B) 120 C) 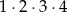 D)
D) 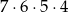
W trapezie prostokątnym krótsza podstawa i dłuższe ramię są równe i mają długość 8 cm. Kąt między dłuższym ramieniem i dłuższą podstawą ma miarę 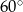 . Pole trapezu jest równe
. Pole trapezu jest równe
A) 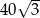 B)
B) 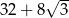 C) 40 D)
C) 40 D) 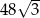
Wartość wyrażenia ![[ ( ) ]1 −2 1 − 1 2 2 + 6](https://img.zadania.info/zes/0099786/HzesT84x.gif) jest równa:
jest równa:
A)  B)
B) 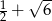 C)
C) 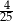 D)
D) 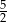
Wielomian 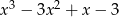 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 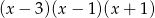
B) 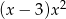
C) 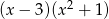
D) 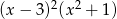
Zadania otwarte
Wierzchołkami trójkąta 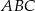 są punkty
są punkty 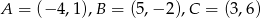 . Oblicz długość środkowej
. Oblicz długość środkowej 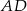 .
.
Wykaż, że liczby 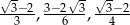 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Rozwiąż nierówność 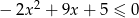 .
.
Wykaż, że dla każdych liczb rzeczywistych  oraz
oraz  prawdziwa jest nierówność
prawdziwa jest nierówność
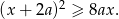
Przyprostokątne trójkąta prostokątnego 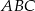 mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta
mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta 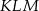 podobnego do trójkąta
podobnego do trójkąta 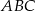 . Oblicz pole trójkąta
. Oblicz pole trójkąta 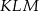 .
.
Kąt rozwarcia stożka jest równy 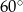 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.
. Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.
Obecnie 1 kg cukru kosztuje o 3,20 zł więcej niż kilka lat temu. Wówczas za kwotę równą 225 zł można było kupić o 80 kg więcej cukru niż obecnie. Ile kosztuje 1 kg cukru obecnie?
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 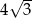 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 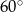 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.

