/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 1443383

Dodaj do ulubionych
Dodaj do rozwiązanych

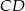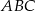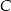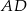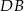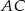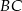Wykaż, że wysokość CD trójkąta prostokątnego ABC poprowadzona z wierzchołka C kąta prostego dzieli przeciwprostokątną na odcinki AD i DB , których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio AC i BC tego trójkąta.

Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

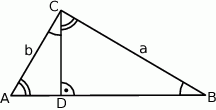
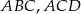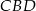Zauważmy, że na powyższym obrazku mamy trzy podobne trójkąty prostokątne: ABC ,ACD i CBD . Z tych podobieństw mamy

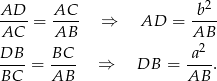
AD-- AC-- -b2- AC = AB ⇒ AD = AB 2 DB--= BC-- ⇒ DB = a--. BC AB AB

Stąd

-b2 2 AD--= AB- = b-. DB -a2 a2 AB
Wersja PDF