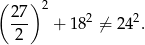Zadanie nr 1848583
Uzasadnij, że nie istnieje trójkąt prostokątny, w którym przeciwprostokątna ma długość 24, a kąty ostre  i
i 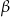 są takie, że
są takie, że 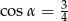 i
i 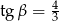 .
.
Rozwiązanie
Najważniejsze przy rozwiązywaniu tego zadania jest ustalenie dlaczego taki trójkąt miałby nie istnieć?
Podane informacje są dwóch typów. Funkcje trygonometryczne kątów zależą tylko od kątów, a więc od kształtu trójkąta, a nie od jego wielkości. Innymi słowy, miary kątów (czy ich funkcje trygonometryczne) nie mają nic do rzeczy z długościami boków (mają za to z ilorazami tych długości). Zatem informacja, że przeciwprostokątna ma długość 24 jest zupełnie bezużyteczna; jeżeli by te warunki z kątami były ok, to istniałby trójkąt o dowolnej przeciwprostokątnej. A jak nie są, to niezależnie od przeciwprostokątnej, takiego trójkąta nie ma.
Kolejne pytanie, to dlaczego warunki z kątami mają uniemożliwiać istnienie trójkąta? Odpowiedź jest bardzo prosta, ponieważ trójkąt ma być prostokątny, to 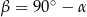 i
i 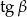 jest jednoznacznie wyznaczony przez
jest jednoznacznie wyznaczony przez 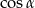 (bo
(bo 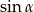 możemy wyliczyć z jedynki trygonometrycznej). Jeżeli trójkąta ma nie być, to widocznie dla podanych liczb się to nie zgadza.
możemy wyliczyć z jedynki trygonometrycznej). Jeżeli trójkąta ma nie być, to widocznie dla podanych liczb się to nie zgadza.
Sposób I
Dobrze, skoro wiemy co mamy zrobić, to robimy – wyliczymy 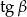 z
z 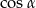 .
.
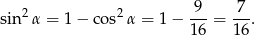
Ponieważ  jest kątem ostrym, mamy stąd
jest kątem ostrym, mamy stąd 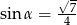 . Możemy teraz wyliczyć
. Możemy teraz wyliczyć 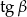 :
:
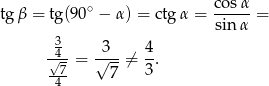
Skoro się nie zgadza, to trójkąta nie ma.
Sposób II
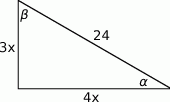
Jeżeli 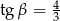 to boki trójkąta mają długości
to boki trójkąta mają długości 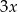 i
i 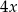 (jak na rysunku). Wtedy z podanego
(jak na rysunku). Wtedy z podanego 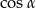 mamy
mamy
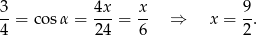
To oznacza, że boki trójkąta mają długości 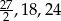 . To jednak nie jest możliwe, bo
. To jednak nie jest możliwe, bo