/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 1956997

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwusieczna kąta ostrego 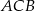ACB przecina przyprostokątną 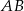AB trójkąta prostokątnego 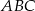ABC w punkcie D .

PIC

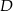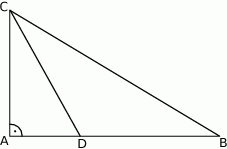
Udowodnij, że jeżeli 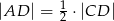|AD | = 12 ⋅|CD | , to |BD | = |CD | .

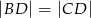Rozwiązanie

W trójkącie prostokątnym 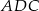ADC mamy

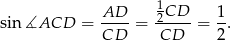
1 sin ∡ACD = AD-- = -2CD- = 1. CD CD 2

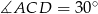Zatem ∘ ∡ACD = 30 oraz

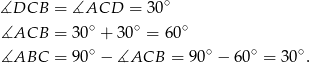
∘ ∡DCB = ∡ACD = 30 ∡ACB = 30∘ + 30∘ = 60 ∘ ∡ABC = 90∘ − ∡ACB = 90∘ − 60∘ = 30 ∘.

W szczególności

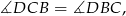
∡DCB = ∡DBC ,

czyli trójkąt 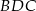BDC jest równoramienny i BD = CD .

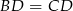Oczywiście zamiast używać funkcji trygonometrycznych mogliśmy też zauważyć, że trójkąt 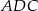ADC jest połówką trójkąta równobocznego.

Wersja PDF