Zadanie nr 2218229
Wykaż, że jeżeli pole koła opisanego na trójkącie prostokątnym jest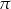 
razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
Rozwiązanie
Oznaczmy długości przyprostokątnych trójkąta przez 
i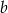 
, a długość przeciwprostokątnej przez 
.
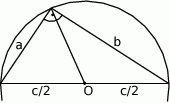
Zauważmy teraz, że okrąg o średnicy będącej przeciwprostokątną trójkąta to dokładnie okrąg opisany na trójkącie (bo kąt oparty na średnicy jest prosty). W takim razie promień tego okręgu to połowa przeciwprostokątnej i podaną informację o polach możemy zapisać w postaci
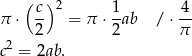
Na mocy twierdzenia Pitagorasa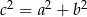 
, więc mamy
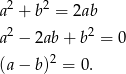
Zatem rzeczywiście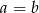 
.
