Zadanie nr 3053531
Okrąg przechodzący przez końce przyprostokątnej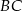 
trójkąta prostokątnego 
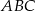przecina drugą przyprostokątną 
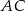oraz przeciwprostokątną 
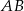tego trójkąta odpowiednio w punktach 
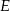i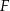 
. Wykaż, że promień okręgu opisanego na trójkącie 
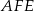jest równy 
.
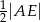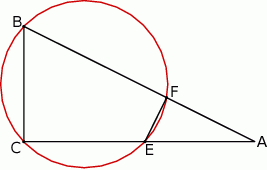
Rozwiązanie
Czworokąt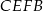 
jest wpisany w okrąg, więc
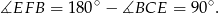
To oznacza, że trójkąt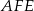 
jest prostokątny i odcinek 
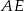jest średnicą okręgu opisanego na tym trójkącie.
