Punkt M przyprostokątnej BC trójkąta prostokątnego ABC zrzutowano... Zadania.info: rozwiązanie zadania, Udowodnij..., 3331119

Zadania.info

Największy internetowy zbiór zadań z matematyki

Rejestracja

Forum

Szukaj

Pomoc

Baza zawiera: 17714 zadań, 1018 zestawów, 35 poradników

cornersUpL

cornersUpR

random

Linki sponsorowane

cornersR

/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 3331119

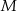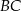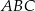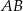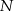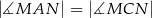Punkt $M$ przyprostokątnej $BC$ trójkąta prostokątnego $ABC$ zrzutowano na przeciwprostokątną $AB$ otrzymując punkt $N$ . Wykaż, że $|∡MAN | = |∡MCN |$ .

Wersja PDF

Rozwiązanie

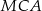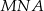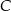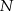Zauważmy, że ponieważ oba kąty $MCA$ i $MNA$ są proste, punkty $C$ i $N$ należą do okręgu o średnicy $AM$ .

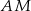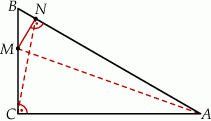
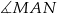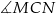W takim razie kąty $∡MAN$ i $∡MCN$ są wpisane w ten okrąg i oparte na tym samym łuku. Są więc równe.

Wersja PDF

Twoje uwagi

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz

Legalni bukmacherzy