/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 5067522

W trójkącie prostokątnym 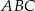ABC przyprostokątne mają długości 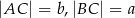|AC | = b,|BC | = a , a wysokość opuszczona z wierzchołka kąta prostego ma długość h .

PIC

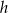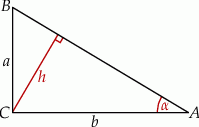
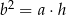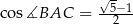Wykaż, że jeżeli b2 = a ⋅h to √- cos ∡BAC = -52−1- .

Wersja PDF

Rozwiązanie

Spróbujemy przekształcić daną równość tak, aby było to wyrażenie, w którym występują tylko funkcje trygonometryczne kąta α .

Mamy

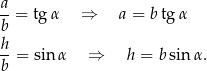
a-= tg α ⇒ a = b tgα b h- b = sin α ⇒ h = bsinα .

Podstawiając to do danej równości mamy

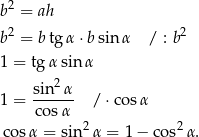
b2 = ah 2 2 b = b tgα ⋅b sin α / : b 1 = tg α sin α 2 1 = sin--α- / ⋅cosα cos α cosα = sin 2α = 1 − co s2α.

Jeżeli podstawimy teraz 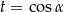t = cosα to mamy równanie kwadratowe

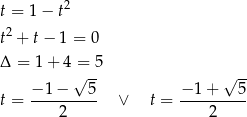
t = 1 − t2 t2 + t − 1 = 0 Δ = 1+ 4 = 5 √ -- √ -- −-1-−---5- −-1+----5- t = 2 ∨ t = 2

Ujemne rozwiązanie odrzucamy i dostajemy 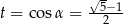√- t = co sα = -5−-1 2 .

Wersja PDF