Zadanie nr 5667295
Trójkąt 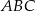 jest prostokątny. Punkt
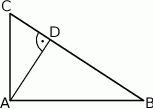
jest prostokątny. Punkt 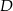 jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 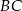 oraz
oraz 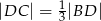 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 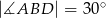 .
.
Rozwiązanie
Zauważmy, że trójkąty 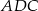 i
i 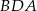 są podobne (bo oba są podobne do trójkąta
są podobne (bo oba są podobne do trójkąta 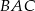 ). Z tego podobieństwa mamy
). Z tego podobieństwa mamy
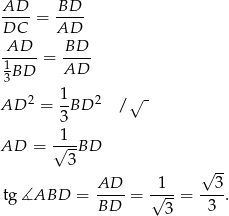
Zatem rzeczywiście 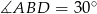 .
.

