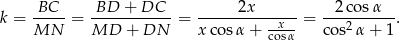Zadanie nr 6776401
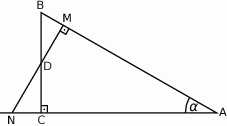
Przez środek  przyprostokątnej
przyprostokątnej  trójkąta prostokątnego
trójkąta prostokątnego  poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 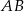 . Prosta ta przecina proste
. Prosta ta przecina proste 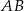 i
i 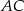 odpowiednio w punktach
odpowiednio w punktach 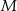 i
i 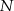 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 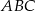 i
i 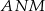 jest równa
jest równa 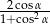 .
.
Rozwiązanie
Zauważmy, że trójkąty 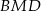 i
i 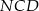 są oba prostokątne i mają wspólny kąt przy wierzchołku
są oba prostokątne i mają wspólny kąt przy wierzchołku 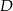 .
.
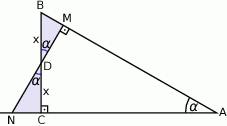
Ponadto
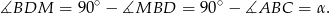
Jeżeli oznaczymy 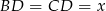 to z trójkątów
to z trójkątów 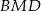 i
i 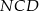 mamy
mamy
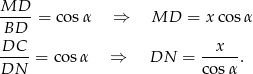
W takim razie skala podobieństwa trójkątów 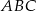 i
i 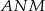 jest równa
jest równa