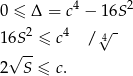/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 8174573

Wykaż, że jeżeli pole trójkąta prostokątnego jest równe 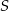S , to długość jego przeciwprostokątnej jest nie mniejsza niż √ -- 2 S .

Wersja PDF

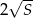Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

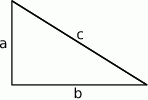
Sposób I

Przekształcamy nierówność, którą mamy udowodnić w sposób równoważny.

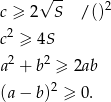
√ -- 2 c ≥ 2 S / () c2 ≥ 4S a2 + b2 ≥ 2ab 2 (a − b) ≥ 0 .

Sposób II

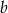Liczby a i b są rozwiązaniami układu równań

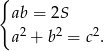
{ ab = 2S a2 + b 2 = c2.

Podstawiamy 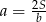a = 2S b z pierwszego równania do drugiego i mamy

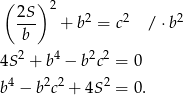
( ) 2 2S- + b2 = c2 / ⋅b 2 b 4S 2 + b4 − b 2c2 = 0 b 4 − b2c2 + 4S 2 = 0.

Jest to równanie dwukwadratowe, więc podstawiamy 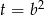t = b2 .

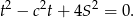
t2 − c2t + 4S2 = 0 .

Równanie to musi mieć rozwiązania, więc musi być spełniony warunek

0 ≤ Δ = c4 − 16S2 2 4 √ - 16S ≤ c / 4 √ -- 2 S ≤ c.
Wersja PDF